题目内容
(理)设数列{an}满足a1=t,a2=t2,前n项和为Sn,且Sn+2-(t+1)Sn+1+tSn=0(n∈N*).(1)证明:数列{an}为等比数列,并求{an}的通项公式;
(2)当![]() <t<2时,比较2n+2-n与tn+t-n的大小;
<t<2时,比较2n+2-n与tn+t-n的大小;
(3)若![]() <t<2,bn=
<t<2,bn=![]() ,求证:
,求证:![]() .
.
(文)设Sn为数列{an}的前n项和,且Sn=![]() (an-1)(n∈N*),数列{bn}的通项公式为bn=4n+3(n∈ N*).
(an-1)(n∈N*),数列{bn}的通项公式为bn=4n+3(n∈ N*).
(1)求数列{an}的通项公式;
(2)若将数列{an}与{bn}的公共项按它们在原来数列中的先后顺序排成一个新数列{dn},证明:数列{dn}的通项公式为dn=32n+1(n∈N*).
答案:(埋)(1)由Sn+2-(t+1)Sn+1+tSn=0,
得(t+1)Sn+1=Sn+2+tSn,即an+2=tan+1,
而a1=t,a2=t2
所以,数列{an}是以t为首项、t为公比的等比数列.
于是an=tn.
(2)∵(tn+t-n)-(2n+2-n)=(tn-2n)[1-![]() ]
]
且![]() <t<2
<t<2
∴![]() <1,∴tn-2n<0且1-(
<1,∴tn-2n<0且1-(![]() )n<0
)n<0
∴(tn-2n)[1-(![]() )n]<0
)n]<0
∴tn+t-n<2n+2-n.
(3)![]() =
=![]() (tn+t-n)
(tn+t-n)
∴2(![]() )<(2+22+…+2n)+(2-1+2-2+…+2-n)=2(2n-1)+1-2-n=2n+1-(1+2-n)<2n+1
)<(2+22+…+2n)+(2-1+2-2+…+2-n)=2(2n-1)+1-2-n=2n+1-(1+2-n)<2n+1 ![]()
∴![]() .
.
(文)(1)∵Sn=![]() (an-1)(n∈N*),
(an-1)(n∈N*),
∴a1=S1=![]() (a1-1),
(a1-1),
∴a1=3.
n≥2时,an=Sn-Sn-1=![]() (an-1)
(an-1)![]() (an-1-1),
(an-1-1),
∴an=3an-1,即![]() =3(n≥2).
=3(n≥2).
∴数列{an}是以3为首项、公比为3的等比数列,
∴an=3·3n-1=3n(n∈N*).
(2)由(1)知a1、a2显然不是数列{bn}中的项.
∵a3=27=4×6+3,
∴d1=27是数列{bn}中的第6项,
设ak=3k是数列{bn}中的第m项,
则3k=4m+3(k、m∈N*).
∵ak+1=3k+1=3×3k=3(4m+3)=4(3m+2)+1,
∴ak+1不是数列{bn}中的项.
∵ak+2=3k+2=9×3k=9(4m+3)=4(9m+6)+3,
∴ak+2是数列{bn}中的项.
∴d1=a3,d2=a5,d3=a7,…,dn=a2n+1,
∴数列{dn}的通项公式是dn=32n+1(n∈N*).

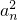 成等差数列.(1)求通项an;(2)设
成等差数列.(1)求通项an;(2)设 求f(n)的最大值.
求f(n)的最大值. 成等差数列.(1)求通项an;(2)设
成等差数列.(1)求通项an;(2)设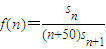 求f(n)的最大值.
求f(n)的最大值.