题目内容
圆 内有一点
内有一点 ,
, 为过点
为过点 且倾斜角为
且倾斜角为 的弦.
的弦.
(1)当 时,求
时,求 ;
;
(2)当弦 被点
被点 平分时,求出直线
平分时,求出直线 的方程;
的方程;
(3)设过 点的弦的中点为
点的弦的中点为 ,求点
,求点 的坐标所满足的关系式.
的坐标所满足的关系式.
(1) ;(2)
;(2) ;(3)
;(3) .
.
解析试题分析:(1)通过倾斜角先求出直线 的方程,然后利用特征三角形求解;
的方程,然后利用特征三角形求解;
(2)由题意知直线 与直线
与直线 垂直,故斜率之积为
垂直,故斜率之积为 ,可通过
,可通过 的斜率求出
的斜率求出 的斜率,进而写出直线
的斜率,进而写出直线 的方程;
的方程;
(3)通过由 、
、 、
、 三点构成的直角三角形,利用勾股定理即可求解.
三点构成的直角三角形,利用勾股定理即可求解.
试题解析:(1)过点 做
做 于
于 ,连结
,连结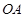 ,当
,当 时,直线
时,直线 的斜率为
的斜率为 ,故直线
,故直线 的方程
的方程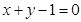 ,∴
,∴
 ,
,
又∵ ,∴
,∴ ,∴
,∴ .
.
(2)当弦 被
被 平分时,
平分时, ,此时
,此时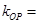
 ,
,
∴ 的点斜式方程为
的点斜式方程为 ,即
,即 .
.
(3)设 的中点为
的中点为 ,则△
,则△ 为直角三角形,故
为直角三角形,故 ,
,
即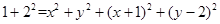 ,整理得
,整理得 .
.
考点:1.弦所在直线方程的求解;2.弦长问题.

练习册系列答案
相关题目
 是直线
是直线
 上一动点,
上一动点,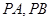 是圆C:
是圆C: 的两条切线,A、B是切点,若四边形
的两条切线,A、B是切点,若四边形 的最小面积是2,则
的最小面积是2,则 的值为?
的值为? 为圆心的圆与直线
为圆心的圆与直线 相切,过点
相切,过点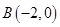 的动直线与圆
的动直线与圆 相交于
相交于 两点.
两点. 时,求直线
时,求直线 的方程.
的方程. (t∈R,t≠0)为圆心的圆与x轴交于点O、A,与y轴交于点O、B,其中O为原点.
(t∈R,t≠0)为圆心的圆与x轴交于点O、A,与y轴交于点O、B,其中O为原点. 和直线
和直线 所得弦长分别为
所得弦长分别为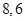 ,求动圆圆心的轨迹方程。
,求动圆圆心的轨迹方程。 .
. 的切线在
的切线在 轴和
轴和 轴上的截距相等,且截距不为零,求此切线的方程;
轴上的截距相等,且截距不为零,求此切线的方程; 向该圆引一条切线,切点为
向该圆引一条切线,切点为 ,
, 为坐标原点,且有
为坐标原点,且有 ,求使
,求使 的长取得最小值的点
的长取得最小值的点 (t∈R,t≠0)为圆心的圆与x轴交于点O,A,与y轴交于点O,B,其中O为原点.
(t∈R,t≠0)为圆心的圆与x轴交于点O,A,与y轴交于点O,B,其中O为原点. 与圆
与圆 外切于点
外切于点 ,直线
,直线 是两圆的外公切线,分别与两圆相切于
是两圆的外公切线,分别与两圆相切于 两点,
两点, 是圆
是圆 作圆
作圆 .
.
 三点共线;
三点共线; .
.