Question

分别求点P(a,b,c)关于坐标平面、坐标轴、坐标原点的对称点的坐标.

Answer 1

思路分析:要认真考虑各情况下的对称点应具有的性质,进而得出对称点与点P的关系.

解:点P(a,b,c)关于原点的对称点为P′(x,y,z),则PP′的中点为(0,0,0),故点P(a,b,c)关于原点的对称点为(-a,-b,-c).

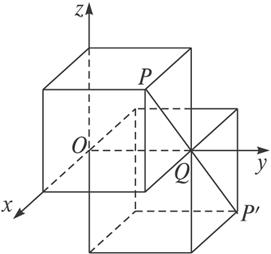
图4-3-1

    点P(a,b,c)关于xOy平面的对称点为P′,则直线PP′垂直于xOy平面,直线上的点的坐标满足x=a,y=b,且线段PP′的中点在xOy平面内(z=0),故点P(a,b,c)关于xOy平面的对称点为(a,b,-c).类似地,点P(a,b,c)关于yOz平面的对称点为(-a,b,c),关于zOx平面的对称点为(a,-b,c).

点P(a,b,c)关于y轴的对称点为P′,线段PP′被y轴垂直平分,过点P作与y轴垂直的平面,与y轴相交于Q(0,a,0),PQ⊥y轴,PP′中点为Q,故点P(a,b,c)关于y轴的对称点为P′(-a,b,-c).

类似地,点P(a,b,c)关于x轴的对称点为P′(a,-b,-c),点P(a,b,c)关于z轴的对称点为P′(-a,-b,c).

  绿色通道:记忆方法:“关于谁谁不变,其余的则相反”,如:关于x轴对称的点,横坐标不变,纵坐标、竖坐标变为原来的相反数;关于xOy坐标平面对称的点,横、纵坐标不变,竖坐标变为原来的相反数.