Question

函数f（x）=|2^x-1|，若a＜b＜c且f（a）＞f（c）＞f（b），则下列四个式子是成立的是（　　）

• A、a＜0，b＜0，c＜0
• B、a＜0，b≥0，c＞0
• C、2^c+2^a＜2
• D、2^-a＜2^c

Answer 1

考点：指数函数的图像变换

专题：函数的性质及应用,不等式的解法及应用

分析：根据指数函数的图象和性质即可得到结论．

解答： 解：f（x）=

2x-1，  x≥0 1-2x，  x＜0

，
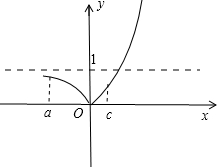
故可作出f（x）=|2^x-1|的图象如图所示，
由图可知，要使a＜b＜c且f（a）＞f（c）＞f（b）成立，则有a＜0且c＞0，
且1-2^a＞2^c-1，
∴2^a+2^c＜2．
故选：C．

点评：本题主要考查不等式的性质的判断，利用指数函数的性质以及基本不等式是解决本题的关键，综合性较强，难度较大．