题目内容
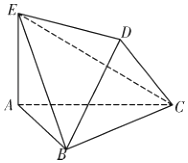
【题目】如图![]() ,四边形
,四边形![]() 中,
中,![]() 是
是![]() 的中点,
的中点,![]() ,
,![]() ,
,![]() ,
,![]() ,将(图
,将(图![]() )沿直线
)沿直线![]() 折起,使
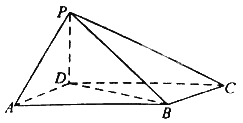
折起,使![]() (如图
(如图![]() ).
).

(1)求证:![]() ;
;
(2)求点![]() 到平面
到平面![]() 的距离.
的距离.
【答案】(1)见解析;(2)![]() .
.
【解析】
(1)取![]() 的中点
的中点![]() ,连接
,连接![]() 、
、![]() ,由已知得
,由已知得![]() ,利用勾股定理证明出
,利用勾股定理证明出![]() ,由中位线的性质得出
,由中位线的性质得出![]() ,由此得出
,由此得出![]() ,利用直线与平面垂直的判定定理证明
,利用直线与平面垂直的判定定理证明![]() 平面
平面![]() ,由此可证明出
,由此可证明出![]() ;
;
(2)证明出![]() 平面
平面![]() ,并计算出
,并计算出![]() 的面积,可计算出三棱锥
的面积,可计算出三棱锥![]() 的体积,并计算出
的体积,并计算出![]() 的面积,再利用等体积法计算出点
的面积,再利用等体积法计算出点![]() 到平面
到平面![]() 的距离.
的距离.
(1)取![]() 中点为
中点为![]() ,连接
,连接![]() 、
、![]() ,
,

在图![]() 中,
中,![]() ,
,![]() 为
为![]() 的中点,则
的中点,则![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() 、
、![]() 分别为
分别为![]() 、
、![]() 的中点,
的中点,![]() ,
,![]() ,
,
![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() ;
;
(2)![]() ,
,![]() ,则
,则![]() ,
,![]() 是等腰直角三角形,
是等腰直角三角形,
![]() 为
为![]() 的中点,
的中点,![]() ,
,
![]() 、
、![]() 分别为
分别为![]() 、
、![]() 的中点,
的中点,![]() ,
,
又![]() ,
,![]() ,
,![]() ,
,
又![]() ,
,![]() ,
,![]() 平面
平面![]() .
.
![]() 的面积为
的面积为![]() ,
,
则三棱锥![]() 的体积为
的体积为![]() .
.
![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() ,
,
![]() 为
为![]() 的中点,
的中点,![]() ,又
,又![]() ,
,![]() ,
,
![]() ,则
,则![]() ,
,
![]() 的面积为
的面积为![]() .
.
设点![]() 到平面
到平面![]() 的距离为
的距离为![]() ,则
,则![]() ,
,
![]() ,因此,点
,因此,点![]() 到平面
到平面![]() 的距离为
的距离为![]() .
.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
【题目】2019年,我国施行个人所得税专项附加扣除办法,涉及子女教育、继续教育、大病医疗、住房贷款利息或者住房租金、赡养老人等六项专项附加扣除.某单位老、中、青员工分别有![]() 人,现采用分层抽样的方法,从该单位上述员工中抽取
人,现采用分层抽样的方法,从该单位上述员工中抽取![]() 人调查专项附加扣除的享受情况.
人调查专项附加扣除的享受情况.
(Ⅰ)应从老、中、青员工中分别抽取多少人?
(Ⅱ)抽取的25人中,享受至少两项专项附加扣除的员工有6人,分别记为![]() .享受情况如右表,其中“
.享受情况如右表,其中“![]() ”表示享受,“×”表示不享受.现从这6人中随机抽取2人接受采访.
”表示享受,“×”表示不享受.现从这6人中随机抽取2人接受采访.
员工 项目 | A | B | C | D | E | F |
子女教育 | ○ | ○ | × | ○ | × | ○ |
继续教育 | × | × | ○ | × | ○ | ○ |
大病医疗 | × | × | × | ○ | × | × |
住房贷款利息 | ○ | ○ | × | × | ○ | ○ |
住房租金 | × | × | ○ | × | × | × |
赡养老人 | ○ | ○ | × | × | × | ○ |
(i)试用所给字母列举出所有可能的抽取结果;
(ii)设![]() 为事件“抽取的2人享受的专项附加扣除至少有一项相同”,求事件
为事件“抽取的2人享受的专项附加扣除至少有一项相同”,求事件![]() 发生的概率.
发生的概率.