题目内容
设x,y∈R,在直角坐标平面内,a=(x,y+2),b=(x,y-2),且|a|+|b|=8.(Ⅰ)求点M(x,y)的轨迹C的方程;
(Ⅱ)过点(0,3)作直线l与曲线C交于A、B两点,若以AB为直径的圆过坐标原点,求直线l的方程.
解:(1)由题意得:![]() =8,即点M(x,y)到两定点F1(0,-2),F2(0,2)的距离之和为定值,且|F1F2|<8,所以点M(x,y)的轨迹是以F1、F2为焦点的椭圆,化简可得椭圆方程为:
=8,即点M(x,y)到两定点F1(0,-2),F2(0,2)的距离之和为定值,且|F1F2|<8,所以点M(x,y)的轨迹是以F1、F2为焦点的椭圆,化简可得椭圆方程为:![]() =1
=1
(Ⅱ)过点(0,3)作直线l,当l与x轴垂直时,AB过坐标原点,这与以AB为直径的圆过坐标原点矛盾.∴直线l的斜率存在.设l的方程为y=kx+3,A(x1,y1),B(x2,y2),
由 消去y得(4+3k2)x2+18kx-21=0.
消去y得(4+3k2)x2+18kx-21=0.
△=(18k)2-4(4+3k2)(-21)>0恒成立.
且x1+x2=![]() ,x1x2=
,x1x2=![]() ,由条件AB为直径,
,由条件AB为直径,
则OA⊥OB,即![]() =0,∴x1x2+y1y2=0,
=0,∴x1x2+y1y2=0,
y1y2=(kx1+3)(kx2+3)=k2x1x2+3k(x1+x2)+9,
即(1+k2)x1x2+3k(x1+x2)+9=0,
∴(1+k2)(![]() )+3k(
)+3k(![]() )+9=0,
)+9=0,
解得:k=±![]() ∴直线l的方程为:y=±
∴直线l的方程为:y=±![]() x+3
x+3

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
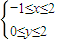 所表示的平面区域是W,从区域W中随机取点M(x,y).
所表示的平面区域是W,从区域W中随机取点M(x,y).