题目内容
已知函数y=x-3+
(x>-1),当x=a时,y取得最小值b,则a+b=
| 9 | x+1 |
4
4
.分析:由y=x-3+
=x+1+
-4,结合已知x的范围,由均值不等式可求函数的最小值及取得最小值时的x,即可求解
| 9 |
| x+1 |
| 9 |
| x+1 |
解答:解:∵y=x-3+
=x+1+
-4,
因为x>-1,所以x+1>0,
>0,
由均值不等式得y=x+1+
-4≥2
-4=2,
当且仅当x+1=
,即(x+1)2=9,
所以x+1=3,x=2时取等号,
所以a=2,b=2,a+b=4.
故答案为:4
| 9 |
| x+1 |
| 9 |
| x+1 |
因为x>-1,所以x+1>0,
| 9 |
| x+1 |
由均值不等式得y=x+1+
| 9 |
| x+1 |
(x+1)×
|
当且仅当x+1=
| 9 |
| x+1 |
所以x+1=3,x=2时取等号,
所以a=2,b=2,a+b=4.
故答案为:4
点评:本题主要考查了基本不等式在求解函数的最值及取得条件的配凑的应用,属于基础试题

练习册系列答案
相关题目
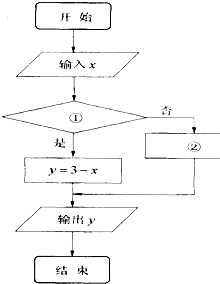 已知函数y=|x-3|,如图,程序框图表示的是给定x值,求其相应函数值的算法.请将该程序框图补充完整,其中①处填
已知函数y=|x-3|,如图,程序框图表示的是给定x值,求其相应函数值的算法.请将该程序框图补充完整,其中①处填