题目内容
求证:(1) ; (2)
; (2)  +
+ >
> +
+ 。
。
 ; (2)
; (2)  +
+ >
> +
+ 。
。(1)根据均值不等式来得到证明,根据 ,
, ,
, 相加得到。
相加得到。
(2)利用分析法两边平方,结合有理数的大小来判定。
 ,
, ,
, 相加得到。
相加得到。(2)利用分析法两边平方,结合有理数的大小来判定。
试题分析:证明:(1) ∵
 ,
, ,
, 将此三式相加得
将此三式相加得 ,∴原式成立 5分
,∴原式成立 5分(2)要证原不等式成立,只需证(
 +
+ )
) >(2
>(2 +
+ )
)
即证
 。∵上式显然成立, ∴原不等式成立. 10分
。∵上式显然成立, ∴原不等式成立. 10分点评:主要是考查了不等式证明,运用分析法和综合法来加以证明,属于基础题。

练习册系列答案
相关题目
 ,则
,则
 ”,其反设正确的是( )
”,其反设正确的是( )



 ,则
,则 或
或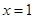 ”时,假设命题的结论不成立的正确叙述是“ ”.
”时,假设命题的结论不成立的正确叙述是“ ”.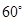 ”时,反设正确的是( )
”时,反设正确的是( ) ,则a,b,c中( )
,则a,b,c中( )