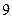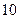题目内容
设等比数列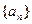 的前n项和为
的前n项和为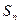 ,等差数列
,等差数列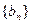 的前n项和为
的前n项和为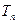 ,已知
,已知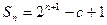 (其中
(其中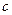 为常数),
为常数),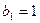 ,
,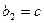 。
。
(1)求常数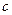 的值及数列
的值及数列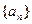 ,
,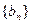 的通项公式
的通项公式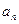 和
和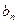 。
。
(2)设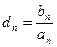 ,设数列
,设数列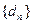 的前n项和为
的前n项和为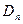 ,若不等式
,若不等式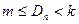 对于任意的
对于任意的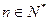 恒成立,求实数m的最大值与整数k的最小值。
恒成立,求实数m的最大值与整数k的最小值。
(3)试比较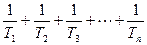 与2的大小关系,并给出证明。
与2的大小关系,并给出证明。
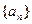 的前n项和为
的前n项和为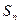 ,等差数列
,等差数列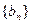 的前n项和为
的前n项和为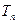 ,已知
,已知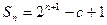 (其中
(其中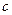 为常数),
为常数),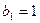 ,
,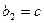 。
。(1)求常数
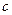 的值及数列
的值及数列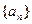 ,
,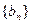 的通项公式
的通项公式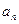 和
和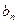 。
。(2)设
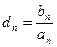 ,设数列
,设数列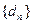 的前n项和为
的前n项和为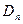 ,若不等式
,若不等式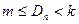 对于任意的
对于任意的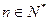 恒成立,求实数m的最大值与整数k的最小值。
恒成立,求实数m的最大值与整数k的最小值。(3)试比较
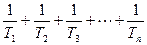 与2的大小关系,并给出证明。
与2的大小关系,并给出证明。 (1)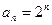 ,
,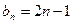 ;(2)3;(3)略
;(2)3;(3)略
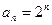 ,
,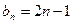 ;(2)3;(3)略
;(2)3;(3)略由题可得当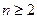 时,
时,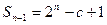
从而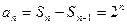 (
(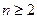 ),
),
又由于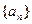 为等比数列,所以
为等比数列,所以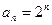 (
(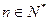 ),
),
所以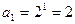 ;另一方面,当
;另一方面,当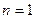 时,
时,

所以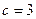 ,从而
,从而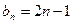
(2 )由(1)得
)由(1)得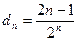
所以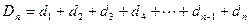
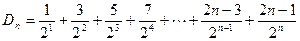 …………①
…………①
从而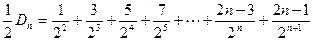 …………②
…………②
①-②得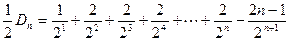
解得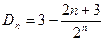
由于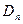 是单调递增的,且
是单调递增的,且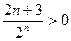 ,所以
,所以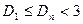 ,即
,即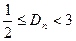
所以实数m的最大值为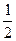 ,整数k的最小值为3.
,整数k的最小值为3.
(3)由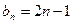 可求得
可求得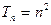 ,
,
当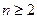 时,
时,
所以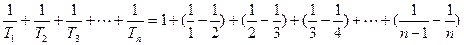
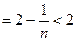
所以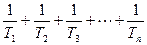
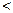 2
2
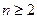 时,
时,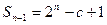
从而
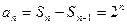 (
(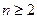 ),
),又由于
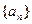 为等比数列,所以
为等比数列,所以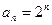 (
(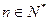 ),
),所以
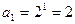 ;另一方面,当
;另一方面,当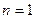 时,
时,

所以
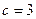 ,从而
,从而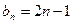
(2
 )由(1)得
)由(1)得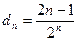
所以
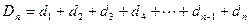
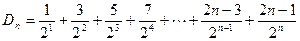 …………①
…………①从而
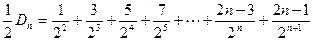 …………②
…………②①-②得
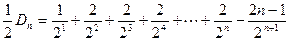
解得
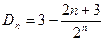
由于
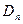 是单调递增的,且
是单调递增的,且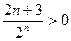 ,所以
,所以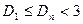 ,即
,即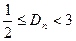
所以实数m的最大值为
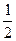 ,整数k的最小值为3.
,整数k的最小值为3.(3)由
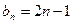 可求得
可求得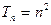 ,
,当
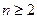 时,
时,
所以
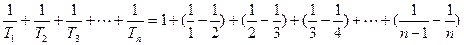
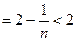
所以
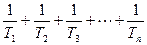
 2
2
练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
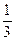 )是函数
)是函数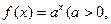 且
且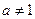 )的图象上一点,等比数列
)的图象上一点,等比数列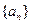 的前
的前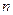 项和为
项和为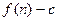 ,数列
,数列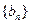
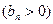 的首项为
的首项为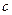 ,且前
,且前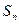 满足
满足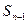 =
=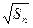 +
+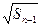 (
(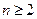 ).
).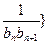 前
前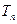 ,问
,问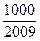 的最小正整数
的最小正整数

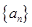 是等差数列,
是等差数列,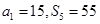 ,则过点
,则过点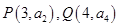 的直线斜率为
的直线斜率为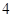
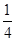
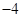
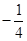
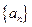 中,
中,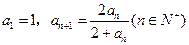 ,则
,则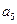 等于______ _.
等于______ _.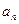 }的首项为
}的首项为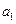 =
=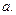 公比为q,则
公比为q,则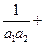
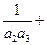 …
…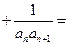 __________。
__________。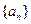 中,
中,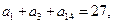 则其前11项的和
则其前11项的和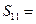 ( )
( )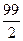
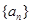 中,已知
中,已知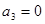 ,
,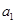 =4,则公差d等于 ( )
=4,则公差d等于 ( )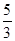 C.- 2 D 3
C.- 2 D 3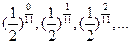 ,则使这个数列前
,则使这个数列前 项的积不小于
项的积不小于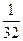 的最大正数
的最大正数