题目内容
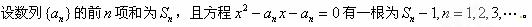
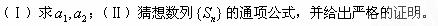
解:(Ⅰ)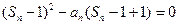 即
即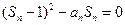
令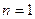
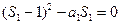 解得
解得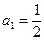
令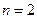
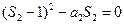 解得
解得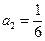
(Ⅱ)解法一: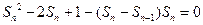
化简得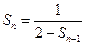
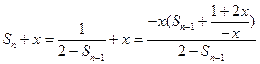
令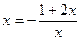 解得
解得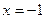
所以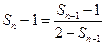
令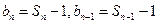
所以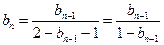 化简
化简 得
得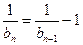
而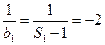
所以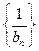 是以-2为首项,-1为公差的等差数列
是以-2为首项,-1为公差的等差数列
所以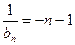 得
得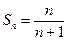
解法二:猜想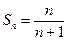 ,下面用数学归纳法证明:
,下面用数学归纳法证明:
(1) 当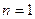 时,
时,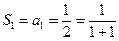 ,所以当
,所以当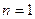 时猜想成立
时猜想成立
(2) 假设当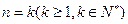 时,猜想成立
时,猜想成立
即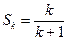
那么当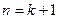 时,
时,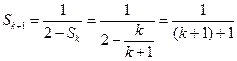
所以当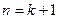 时猜想成立。[来源:学*科*网]
时猜想成立。[来源:学*科*网]
综合(1)、(2)可得对于任意的正整数猜想都成立。
解析

练习册系列答案
相关题目
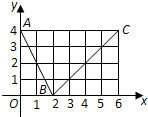 如图,函数f(x)的图象是折线段ABC,其中A,B,C的坐标分别为(0,4),(2,0),(6,4),则f(f(0))=
如图,函数f(x)的图象是折线段ABC,其中A,B,C的坐标分别为(0,4),(2,0),(6,4),则f(f(0))=