题目内容
已知两定点F1(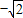 ,0),F2(
,0),F2(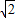 ,0)满足条件
,0)满足条件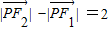 的点P的轨迹方程是曲线C,直线y=kx-2与曲线C交于A、B两点,且
的点P的轨迹方程是曲线C,直线y=kx-2与曲线C交于A、B两点,且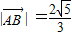 .
.(1)求曲线C的方程;
(2)若曲线C上存在一点D,使
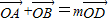 ,求m的值及点D到直线AB的距离.
,求m的值及点D到直线AB的距离.
【答案】分析:(1)由已知两定点F1( ,0),F2(
,0),F2( ,0)满足条件
,0)满足条件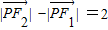 ,可知轨迹为焦点在x轴上的双曲线的左支,进而可求曲线C的方程;
,可知轨迹为焦点在x轴上的双曲线的左支,进而可求曲线C的方程;
(2)将直线方程代入双曲线的方程,利用弦长公式求AB的长,从而可得直线的斜率,进而利用向量求出点D的坐标,利用D满足曲线C的方程,即可求m的值及点D到直线AB的距离.
解答:解:(1)由已知两定点F1(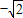 ,0),F2(
,0),F2(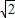 ,0)满足条件
,0)满足条件 ,可知轨迹为焦点在x轴上的双曲线的左支.
,可知轨迹为焦点在x轴上的双曲线的左支.
∵2a=2,∴a=1,
∵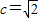 ,∴b2=c2=a2=1
,∴b2=c2=a2=1
∴曲线C的方程为x2-y2=1(x≤-1)
(2)由 得(1-k2)x2+4kx-5=0,
得(1-k2)x2+4kx-5=0,
设A(x1,y1),B(x2,y2)
则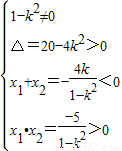 ,解之得
,解之得
∴ ,解之得k2=4
,解之得k2=4
又∵
∴k=-2
∴
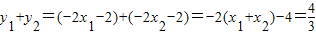
由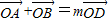 得
得 ,即
,即
∵D在x2-y2=1(x≤-1)上,
∴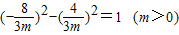 ,∴
,∴
∴D( )
)
∵直线AB:2x+y+2=0
∴点D到直线AB的距离为
点评:本题重点考查双曲线的轨迹方程,考查直线与双曲线的位置关系,考查弦长公式,考查点到直线的距离公式,综合性较强.
 ,0),F2(
,0),F2( ,0)满足条件
,0)满足条件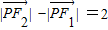 ,可知轨迹为焦点在x轴上的双曲线的左支,进而可求曲线C的方程;
,可知轨迹为焦点在x轴上的双曲线的左支,进而可求曲线C的方程;(2)将直线方程代入双曲线的方程,利用弦长公式求AB的长,从而可得直线的斜率,进而利用向量求出点D的坐标,利用D满足曲线C的方程,即可求m的值及点D到直线AB的距离.
解答:解:(1)由已知两定点F1(
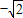 ,0),F2(
,0),F2(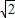 ,0)满足条件
,0)满足条件 ,可知轨迹为焦点在x轴上的双曲线的左支.
,可知轨迹为焦点在x轴上的双曲线的左支.∵2a=2,∴a=1,
∵
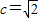 ,∴b2=c2=a2=1
,∴b2=c2=a2=1∴曲线C的方程为x2-y2=1(x≤-1)
(2)由
 得(1-k2)x2+4kx-5=0,
得(1-k2)x2+4kx-5=0,设A(x1,y1),B(x2,y2)
则
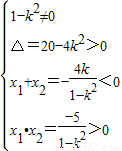 ,解之得
,解之得
∴
 ,解之得k2=4
,解之得k2=4又∵

∴k=-2
∴

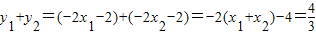
由
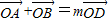 得
得 ,即
,即
∵D在x2-y2=1(x≤-1)上,
∴
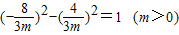 ,∴
,∴
∴D(
 )
) ∵直线AB:2x+y+2=0
∴点D到直线AB的距离为

点评:本题重点考查双曲线的轨迹方程,考查直线与双曲线的位置关系,考查弦长公式,考查点到直线的距离公式,综合性较强.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目