题目内容
【题目】设![]() 实数
实数![]() 满足
满足![]() ,其中
,其中![]() .
.![]() 实数
实数![]() 满足
满足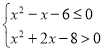 .
.
(1)若![]() ,且
,且![]() 为真,求实数
为真,求实数![]() 的取值范围;
的取值范围;
(2)非![]() 是非
是非![]() 的充分不必要条件,求实数
的充分不必要条件,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)将![]() 代入
代入![]() 中的不等式,并解出该不等式,同时也解出
中的不等式,并解出该不等式,同时也解出![]() 中的不等式组,由
中的不等式组,由![]() 为真,可知
为真,可知![]() 、
、![]() 均为真命题,将
均为真命题,将![]() 、
、![]() 中的不等式(组)的解集取交集可得出实数
中的不等式(组)的解集取交集可得出实数![]() 的取值范围;
的取值范围;
(2)求出非![]() 与非
与非![]() 中
中![]() 的取值范围,结合已知条件转化为两集合的包含关系,可得出关于实数
的取值范围,结合已知条件转化为两集合的包含关系,可得出关于实数![]() 的不等式组,即可解得实数
的不等式组,即可解得实数![]() 的取值范围.
的取值范围.
(1)当![]() 时,解不等式
时,解不等式![]() ,解得
,解得![]() ,即
,即![]() .
.
解不等式![]() ,解得
,解得![]() ,解不等式
,解不等式![]() ,解得
,解得![]() 或
或![]() ,
,![]() .
.
![]() ,若
,若![]() 为真,则
为真,则![]() 、
、![]() 均为真命题,
均为真命题,
此时,实数![]() 的取值范围是
的取值范围是![]() ;
;
(2)当![]() 时,解不等式
时,解不等式![]() ,解得
,解得![]() ,即
,即![]() ,
,
则非![]() 或
或![]() ,非
,非![]() 或
或![]() .
.
因为非![]() 是非
是非![]() 的充分不必要条件,则
的充分不必要条件,则![]() 或
或![]()
![]() 或
或![]() ,
,
所以,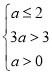 ,解得
,解得![]() .
.
因此,实数![]() 的取值范围是
的取值范围是![]() .
.

练习册系列答案
相关题目