题目内容

8．已知数列{an}的前n项和为Sn，a1=1．当n≥2时，an+2SN-1=2n+1，则S299=（　　）
A．246B．299C．247D．248

分析 通过an+2Sn-1=2n+1与an+1+2Sn=2（n+1）+1作差可知an+1+an=2（n≥2），进而利用分组法求和即可．

解答 解：∵an+2Sn-1=2n+1，an+1+2Sn=2（n+1）+1，
两式相减得：an+1+2an-an=2，即an+1+an=2（n≥2），
又∵a1=1，
∴S299=a1+（a2+a3）+（a4+a5）+…+（a298+a299）
=1+2•$\frac{298}{2}$
=299，
故选：B．

点评 本题考查数列的求和，考查分组法求和，注意解题方法的积累，属于中档题．

练习册系列答案
相关题目
4．设$\overrightarrow{a}$，$\overrightarrow{b}$是不共线的两个向量，已知$\overrightarrow{AB}$=2k$\overrightarrow{a}$+（k2-2）$\overrightarrow{b}$，$\overrightarrow{BC}$=$\overrightarrow{a}$+$\overrightarrow{b}$，$\overrightarrow{CD}$=$\overrightarrow{a}$-2$\overrightarrow{b}$，若A、B、D三点共线，求k的值．
5．若一组数据2，4，6，8的中位数、方差分别为m，n，且ma+nb=1（a＞0，b＞0），则$\frac{1}{a}$+$\frac{1}{b}$的最小值为（　　）
A．6+2$\sqrt{3}$B．4$+3\sqrt{5}$C．9$+4\sqrt{5}$D．20
16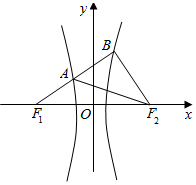．已知F1，F2分别为双曲线C：$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的左、右焦点，若存在过F1的直线分别交双曲线C的左、右支于A，B两点，使得∠BAF2=∠BF2F1，则双曲线C的离心率e的取值范围是（　　）
A．（3，+∞）B．（1，2+$\sqrt{5}$）C．（3，2+$\sqrt{5}$）D．（1，3）
3．若x，y满足不等式组$\left\{\begin{array}{l}y-2≥0\\ x-y+1≥0\\ x+y-5≤0\end{array}\right.$，则$\frac{y}{x}$的最大值是（　　）
A．$\frac{3}{2}$B．1C．2D．3
13．若复数z满足z=$\frac{|8+6i|}{6-8i}$（i是虚数单位），则z的虚部为（　　）
A．4B．$\frac{4}{5}$C．-4D．-$\frac{4}{5}$
20．已知F1，F2分别是双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a，b＞0）的左．右焦点，且|F1F2|=2，若P是该双曲线右支上的一点，且满足|PF1|=2|PF2|，则△PF1F2面积的最大值是（　　）
A．2B．$\frac{5}{3}$C．$\frac{4}{3}$D．1
17．已知数列{an}中，对任意的n∈N*，若满足an+an+1+an+2=s（s为常数），则称该数列为3阶等和数列，其中s为3阶公和；若满足an•an+1=t（t为常数），则称该数列为2阶等积数列，其中t为2阶公积．已知数列{pn}为首项为1的3阶等和数列，且满足$\frac{p_3}{p_2}=\frac{p_2}{p_1}=2$；数列{qn}为首项为-1，公积为2的2阶等积数列，设Sn为数列{pn•qn}的前n项和，则S2016=-7056．
18．已知复数w满足w-1=（1+w）i（i为虚数单位），则w=（　　）
A．1-iB．-iC．-1+iD．i

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网