题目内容
设△ABC三个角A,B,C的对边分别为a,b,c,向量 ,
, ,且
,且 .
.
(Ⅰ)求角B的大小;
(Ⅱ)若△ABC是锐角三角形, ,求
,求 的取值范围.
的取值范围.
(Ⅰ) 或
或 .(Ⅱ)
.(Ⅱ) .
.
解析试题分析:(Ⅰ)∵  ,
, ,且
,且 ,
,
∴ a-2bsinA = 0,由正弦定理得 sinA-2sinB sinA = 0. 3分
∵ 0<A,B,C<p,∴  ,得
,得  或
或 . 5分
. 5分
(Ⅱ)∵ △ABC是锐角三角形,∴  , -6分
, -6分
∴  ,即
,即  . -12分
. -12分
考点:平面向量的坐标运算,向量平行的条件,正弦定理的应用,两角和差的三角函数,三角函数的性质。
点评:中档题,本题难度不大,但考查知识较为全面,综合考查了平面向量的坐标运算,向量平行的条件,正弦定理的应用,两角和差的三角函数,三角函数的性质。在三角形中,角的范围受到了限制,确定三角函数值范围时,要特别注意。

练习册系列答案
相关题目
 中,内角
中,内角 的对边分别为
的对边分别为 ,且
,且 ,
, .
. 的大小;
的大小;  ,求
,求 ,求塔高AB.
,求塔高AB.
 、
、 、
、 所对的边分别为
所对的边分别为 、
、 、
、 ,已知向量
,已知向量 ,且
,且 .
. ,
, ,求△ABC的面积.
,求△ABC的面积.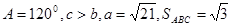 ,求
,求 。
。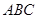 内的空地上植造“绿地
内的空地上植造“绿地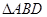 ”,其中
”,其中 ,
,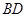 长可根据需要进行调节(
长可根据需要进行调节(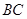 足够长),现规划在
足够长),现规划在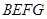 内种花,其余地方种草,设种草的面积
内种花,其余地方种草,设种草的面积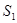 与种花的面积
与种花的面积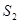 的比
的比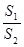 为
为 ,
,
 ,将
,将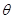 的函数关系;
的函数关系;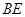 为多长时,
为多长时, 与
与 的距离,由于地形的限制,需要在岸上选取
的距离,由于地形的限制,需要在岸上选取 和
和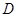 两点,现测得
两点,现测得 ,
, ,
, ,
, ,
, ,试求两景点
,试求两景点
 米,如图,同时也能测量出
米,如图,同时也能测量出 ,
, ,
,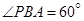 ,
, ,则P、Q两棵树和A、P两棵树之间的距离各为多少?
,则P、Q两棵树和A、P两棵树之间的距离各为多少?
 所对的边分别是
所对的边分别是 ,且
,且 。
。 的值;
的值; ,
, 的面积
的面积 ,求
,求 的值。
的值。