题目内容
设函数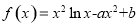 在点
在点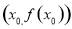 处的切线方程为
处的切线方程为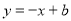 .
.
(1)求实数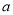 及
及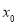 的值;
的值;
(2)求证:对任意实数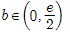 ,函数
,函数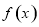 有且仅有两个零点.
有且仅有两个零点.
(1)  (2)详见解析
(2)详见解析
【解析】
试题分析:(1) 由导数几何意义得: ,
, ,又
,又 ,
, ,解得
,解得 (2)先根据导数确定函数走势:
(2)先根据导数确定函数走势: 在
在 上单调减,在
上单调减,在 上单调增,
上单调增, 有最小值
有最小值 ,因为
,因为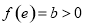 ,所以
,所以 在
在 上一定有一解,在
上一定有一解,在 上有且仅有一解;难点在证明存在
上有且仅有一解;难点在证明存在 使
使 ,这时需构造一个函数
,这时需构造一个函数 易得
易得 ,从而
,从而 ,取
,取 ,从而得证.
,从而得证.
试题解析:(1)  2分
2分
所以在点 处的切线方程为
处的切线方程为
其中 ,
, 4分
4分
解得 6分
6分
(2) 
当 时
时 ,
, 在
在 上单调减
上单调减
当 时
时 ,
, 在
在 上单调增
上单调增
所以 有最小值
有最小值 8分
8分
又 ,所以
,所以 在
在 上一定有一解 10分
上一定有一解 10分
下面证明存在 使
使
令 ,
,
所以当 时,
时, 在
在 上单调减
上单调减
当 时,
时, ,
,
取 12分
12分
所以 在
在 上一定有一解 14分
上一定有一解 14分
综上所述,函数 在
在 上有且仅有两个零点. 16分
上有且仅有两个零点. 16分
考点:导数几何意义,导数应用

练习册系列答案
相关题目
 ,则输出的
,则输出的

 B.
B.  C.
C.  D.
D. 
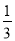 ,且各人能否通过测试是相互独立的,则至少有一位同学能通过测试的概率为
,且各人能否通过测试是相互独立的,则至少有一位同学能通过测试的概率为 B.
B. 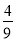 C.
C. 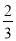 D.
D. 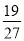
 的首项
的首项 ,前
,前 项和为
项和为 ,且满足
,且满足 ,则满足
,则满足 的
的 的最大值为
的最大值为  本不同的数学书和
本不同的数学书和 本语文书在书架上随机排成一行,则
本语文书在书架上随机排成一行,则 本数学书相邻的概率为
本数学书相邻的概率为  .
. 时,求
时,求 的值;
的值; ,当
,当 时,求
时,求 的值域.
的值域. 中,
中, 分别为
分别为 的中点,记三棱锥
的中点,记三棱锥 的体积为
的体积为 ,
, 的体积为
的体积为 ,则
,则
 是奇函数,则
是奇函数,则
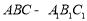 中,
中,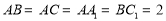 ,
, 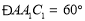 ,平面
,平面 平面
平面 ,
, 与
与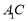 相交于点
相交于点 .
.
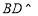 平面
平面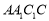 ;
;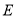 是直线
是直线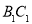 上一点,且
上一点,且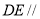 平面
平面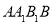 ,求平面
,求平面 与平面
与平面 夹角的余弦值.
夹角的余弦值.