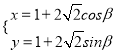题目内容
【题目】已知平面向量 ![]() ,
, ![]() (
( ![]() ≠
≠ ![]() )满足
)满足 ![]() =2,且
=2,且 ![]() 与
与 ![]() ﹣
﹣ ![]() 的夹角为120° , t∈R,则|(1﹣t)
的夹角为120° , t∈R,则|(1﹣t) ![]() +t
+t ![]() |的最小值是 . 已知
|的最小值是 . 已知 ![]()
![]() =0,向量
=0,向量 ![]() 满足(
满足( ![]() ﹣
﹣ ![]() )(
)( ![]() ﹣
﹣ ![]() )=0,|
)=0,| ![]() ﹣
﹣ ![]() |=5,|
|=5,| ![]() ﹣
﹣ ![]() |=3,则
|=3,则 ![]()
![]() 的最大值为 .
的最大值为 .
【答案】![]() ;18
;18
【解析】解:①∵平面向量 ![]() 满足|
满足| ![]() |=2,且
|=2,且 ![]() 与
与 ![]() ﹣
﹣ ![]() 的夹角为120°,
的夹角为120°,
故当t( ![]() ﹣
﹣ ![]() )满足t|
)满足t| ![]() ﹣
﹣ ![]() |=
|= ![]() 时,|(1﹣t)
时,|(1﹣t) ![]() +t
+t ![]() |(t∈R)取最小值,
|(t∈R)取最小值,
此时由向量加法的三角形法则可得|(1﹣t) ![]() +
+ ![]() |(t∈R)的最小值是
|(t∈R)的最小值是 ![]() ;
;
②由 ![]()
![]() =0,建立如图所示的直角坐标系;
=0,建立如图所示的直角坐标系;
可设 ![]() =(m,0),
=(m,0), ![]() =(0,n),
=(0,n), ![]() =(x,y),
=(x,y),
∵| ![]() ﹣
﹣ ![]() |=5,
|=5,
∴m2+n2=25,记此圆为⊙M;
∵向量 ![]() 满足(
满足( ![]() ﹣
﹣ ![]() )(
)( ﹣
![]() )=0,
)=0,
∴x2+y2﹣mx﹣ny=0,
化为 ![]() +
+ ![]() =
= ![]() ,
,
说明点C在⊙M上;
∴| ![]() |=|
|=| ![]() ﹣
﹣ ![]() |=3,
|=3,
∴| ![]() |=|
|=| ![]() ﹣
﹣ ![]() |=4,
|=4,
过点C分别作CD⊥y轴,CE⊥x轴,垂足分别为D,E;
设∠CBD=θ,则∠OAC=θ,
则x=4sinθ=m﹣3cosθ,
∵ ![]()
![]() =mx=4sinθ(4sinθ+3cosθ)
=mx=4sinθ(4sinθ+3cosθ)
=16sin2θ+12sinθcosθ
=8(1﹣cos2θ)+6sin2θ
=10sin(2θ﹣φ)+8≤18;
∴ ![]()
![]() 的最大值为18.
的最大值为18.
所以答案是: ![]() ,18.
,18.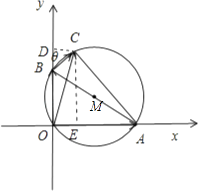

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目