题目内容
在某市组织的一次数学竞赛中全体参赛学生的成绩近似服从正态分布N(60,100),已知成绩在90分以上(含90分)的学生有13人.
(1)求此次参加竞赛的学生总数共有多少人?
(2)若计划奖励竞赛成绩排在前228名的学生,问受奖学生的分数线是多少?
(1) 10000人 (2) 80分
解析解:(1)设学生的成绩为X,共有n人参加竞赛,
∵X~N(60,100),∴μ=60,σ=10.
∴P(X≥90)= [1-P(30<X<90)]
[1-P(30<X<90)]
= (1-0.9974)=0.0013.
(1-0.9974)=0.0013.
又P(X≥90)= ,∴
,∴ =0.0013.∴n=10000.
=0.0013.∴n=10000.
故此次参加竞赛的学生总数共有10000人.
(2)设受奖的学生的分数线为x0.
则P(X≥x0)= =0.0228.
=0.0228.
∵0.0228<0.5,∴x0>60.
∴P(120-x0<X<x0)=1-2P(X≥x0)=0.9544,
∴x0=60+20=80.故受奖学生的分数线是80分.

练习册系列答案
相关题目
某单位从一所学校招收某类特殊人才.对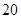 位已经选拔入围的学生进行运动协调能力和逻辑思维能力的测试,其测试结果如下表:
位已经选拔入围的学生进行运动协调能力和逻辑思维能力的测试,其测试结果如下表:
 | 一般 | 良好 | 优秀 |
| 一般 |  |  |  |
| 良好 | 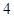 |  |  |
| 优秀 |  |  | 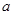 |
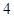 人.由于部分数据丢失,只知道从这
人.由于部分数据丢失,只知道从这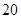 位参加测试的学生中随机抽取一位,抽到逻辑思维能力优秀的学生的概率为
位参加测试的学生中随机抽取一位,抽到逻辑思维能力优秀的学生的概率为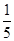 .
.(1)求
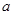 ,
, 的值;
的值;(2)从运动协调能力为优秀的学生中任意抽取
 位,求其中至少有一位逻辑思维能力优秀的学生的概率.
位,求其中至少有一位逻辑思维能力优秀的学生的概率. 某大厦的一部电梯从底层出发后只能在第18,19,20层可以停靠,若该电梯在底层载有5位乘客,且每位乘客在这三层的每一层下电梯的概率均为 ,用X表示这5位乘客在第20层下电梯的人数,求随机变量X的分布列.
,用X表示这5位乘客在第20层下电梯的人数,求随机变量X的分布列.
甲、乙两名射手各打了10发子弹,其中甲击中环数与次数如下表
| 环数 | 5 | 6 | 7 | 8 | 9 | 10 |
| 次数 | 1 | 1 | 1 | 1 | 2 | 4 |
| 环数 | 7 | 8 | 9 | 10 |
| 概率 | 0.2 | 0.3 | p | 0.1 |
(2)比较甲,乙两人射击水平的优劣.
 ,乙的命中率为P2,在射击比赛活动中每人射击两发子弹则完成一次检测,在一次检测中,若两人命中数相等且都不少于一发,则称该射击小组为“先进和谐组”.
,乙的命中率为P2,在射击比赛活动中每人射击两发子弹则完成一次检测,在一次检测中,若两人命中数相等且都不少于一发,则称该射击小组为“先进和谐组”. ,求该小组在一次检测中荣获“先进和谐组”的概率;
,求该小组在一次检测中荣获“先进和谐组”的概率;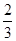 ,且相互间没有影响.
,且相互间没有影响.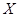 ,试求
,试求