题目内容
某单位从一所学校招收某类特殊人才.对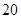 位已经选拔入围的学生进行运动协调能力和逻辑思维能力的测试,其测试结果如下表:
位已经选拔入围的学生进行运动协调能力和逻辑思维能力的测试,其测试结果如下表:
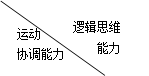 | 一般 | 良好 | 优秀 |
| 一般 |  |  |  |
| 良好 | 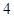 |  |  |
| 优秀 |  |  | 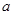 |
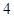 人.由于部分数据丢失,只知道从这
人.由于部分数据丢失,只知道从这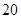 位参加测试的学生中随机抽取一位,抽到逻辑思维能力优秀的学生的概率为
位参加测试的学生中随机抽取一位,抽到逻辑思维能力优秀的学生的概率为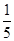 .
.(1)求
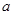 ,
, 的值;
的值;(2)从运动协调能力为优秀的学生中任意抽取
 位,求其中至少有一位逻辑思维能力优秀的学生的概率.
位,求其中至少有一位逻辑思维能力优秀的学生的概率.
(1) ,
, ;(2)
;(2) .
.
解析试题分析:(1)求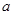 ,
, 的值,由题意,从这
的值,由题意,从这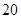 位参加测试的学生中随机抽取一位,抽到逻辑思维能力优秀的学生的概率为
位参加测试的学生中随机抽取一位,抽到逻辑思维能力优秀的学生的概率为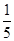 ,而由表中数据可知,运动协调能力或逻辑思维能力优秀的学生共有
,而由表中数据可知,运动协调能力或逻辑思维能力优秀的学生共有 人,可由
人,可由 ,解出
,解出 的值,从而得
的值,从而得 的值;(2)从运动协调能力为优秀的学生中任意抽取
的值;(2)从运动协调能力为优秀的学生中任意抽取 位,求其中至少有一位逻辑思维能力优秀的学生的概率,这显然是古典概型,由题意,运动协调能力为优秀的学生共有
位,求其中至少有一位逻辑思维能力优秀的学生的概率,这显然是古典概型,由题意,运动协调能力为优秀的学生共有 位,列出从
位,列出从 人中任意抽取
人中任意抽取 人的方法,得方法数,找出至少有一位逻辑思维能力优秀的学生的方法数,由古典概型,可求出至少有一位逻辑思维能力优秀的学生的概率.
人的方法,得方法数,找出至少有一位逻辑思维能力优秀的学生的方法数,由古典概型,可求出至少有一位逻辑思维能力优秀的学生的概率.
试题解析:(I)由题意可知,逻辑思维能力优秀的学生共有 人.
人.
设事件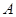 :从
:从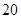 位学生中随机抽取一位,逻辑思维能力优秀的学生,
位学生中随机抽取一位,逻辑思维能力优秀的学生,
则 .解得
.解得  .所以
.所以 . 5分
. 5分
(2)由题意可知,运动协调能力为优秀的学生共有 位,分别记为
位,分别记为 .其中
.其中 和
和 为运动协调能力和逻辑思维能力都优秀的学生.
为运动协调能力和逻辑思维能力都优秀的学生.
从中任意抽取 位,可表示为
位,可表示为 ,
,
 ,
, ,
, ,共
,共 种可能.
种可能.
设事件 :从运动协调能力为优秀的学生中任意抽取
:从运动协调能力为优秀的学生中任意抽取 位,其中至少有一位逻辑思维能力优秀的学生.
位,其中至少有一位逻辑思维能力优秀的学生.
事件 包括
包括 ,
, ,
, ,
, ,共
,共 种可能.所以
种可能.所以 .
.
所以至少有一位逻辑思维能力优秀的学生的概率为 . 13分
. 13分
考点:古典概型.

练习册系列答案
相关题目
为了解甲、乙两个快递公司的工作状况,假设同一个公司快递员的工作状况基本相同,现从甲、乙两公司各随机抽取一名快递员,并从两人某月(30天)的快递件数记录结果中随机抽取10天的数据,制表如下:
| 甲公司某员工A | | 乙公司某员工B | ||||||||||||
| 3 | 9 | 6 | 5 | 8 | 3 | 3 | 2 | 3 | 4 | 6 | 6 | 6 | 7 | 7 |
| | | | | | | 0 | 1 | 4 | 4 | 2 | 2 | 2 | | |
甲公司规定每件4.5元;乙公司规定每天35件以内(含35件)的部分每件4元,超出35件的部分每件7元.
(1)根据表中数据写出甲公司员工A在这10天投递的快递件数的平均数和众数;
(2)为了解乙公司员工B的每天所得劳务费的情况,从这10天中随机抽取1天,他所得的劳务费记为
 (单位:元),求
(单位:元),求 的分布列和数学期望;
的分布列和数学期望;(3)根据表中数据估算两公司的每位员工在该月所得的劳务费.
 月
月 日至
日至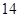 日的空气质量指数趋势图,空气质量指数(
日的空气质量指数趋势图,空气质量指数(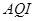 )小于
)小于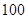 表示空气质量优良,空气质量指数大于
表示空气质量优良,空气质量指数大于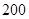 表示空气重度污染,某人随机选择
表示空气重度污染,某人随机选择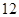 日中的某一天到达该市,并停留
日中的某一天到达该市,并停留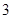 天.
天.
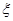 是此人停留期间空气重度污染的天数,求
是此人停留期间空气重度污染的天数,求
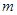 元,正确回答问题B可获奖金
元,正确回答问题B可获奖金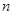 元.活动规定:参与者可任意选择回答问题的顺序,如果第一个问题回答错误,则该参与者猜奖活动中止.假设一个参与者在回答问题前,对这两个问题都很陌生,试确定哪种回答问题的顺序能使该参与者获奖金额的期望值较大.
元.活动规定:参与者可任意选择回答问题的顺序,如果第一个问题回答错误,则该参与者猜奖活动中止.假设一个参与者在回答问题前,对这两个问题都很陌生,试确定哪种回答问题的顺序能使该参与者获奖金额的期望值较大. ,中奖可以获得2分;方案乙的中奖率为
,中奖可以获得2分;方案乙的中奖率为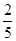 ,中奖可以得3分;未中奖则不得分.每人有且只有一次抽奖机会,每次抽奖中奖与否互不影响,晚会结束后凭分数兑换奖品.若小明选择方案甲抽奖,小红选择方案乙抽奖,记他们的累计得分为X,求X≤3的概率.
,中奖可以得3分;未中奖则不得分.每人有且只有一次抽奖机会,每次抽奖中奖与否互不影响,晚会结束后凭分数兑换奖品.若小明选择方案甲抽奖,小红选择方案乙抽奖,记他们的累计得分为X,求X≤3的概率.