题目内容
5.已知△ABC中,内角A,B,C所对的边分别为a,b,c,且满足asinA-csinC=(a-b)sinB.(1)求角C的大小;
(2)若边长$c=\sqrt{3}$,求△ABC的周长最大值.
分析 (1)通过正弦定理化简已知表达式,然后利用余弦定理求出C的余弦值,得到C的值.
(2)由已知利用正弦定理可得a=2sinA,b=2sin($\frac{2π}{3}$-A),利用三角函数恒等变换的应用化简可求a+b+c=2$\sqrt{3}$sin(A+$\frac{π}{6}$)+$\sqrt{3}$,根据A+$\frac{π}{6}$ 的范围,利用正弦函数的图象和性质得到结果.
解答 解:(1)由已知,根据正弦定理,asinA-csinC=(a-b)sinB
得,a2-c2=(a-b)b,即a2+b2-c2=ab.
由余弦定理得cosC=$\frac{{a}^{2}+{b}^{2}-{c}^{2}}{2ab}$=$\frac{1}{2}$.
又C∈(0,π).
所以C=$\frac{π}{3}$.
(2)∵C=$\frac{π}{3}$,$c=\sqrt{3}$,A+B=$\frac{2π}{3}$,
∴$\frac{a}{sinA}=\frac{b}{sinB}=\frac{\sqrt{3}}{\frac{\sqrt{3}}{2}}=2$,可得:a=2sinA,b=2sinB=2sin($\frac{2π}{3}$-A),
∴a+b+c=$\sqrt{3}$+2sinA+2sin($\frac{2π}{3}$-A)
=$\sqrt{3}$+2sinA+2($\frac{\sqrt{3}}{2}$cosA+$\frac{1}{2}$sinA)
=2$\sqrt{3}$sin(A+$\frac{π}{6}$)+$\sqrt{3}$
∵由0<A<$\frac{2π}{3}$ 可知,$\frac{π}{6}$<A+$\frac{π}{6}$<$\frac{5π}{6}$,可得:$\frac{1}{2}$<sin(A+$\frac{π}{6}$)≤1.
∴a+b+c的取值范围(2$\sqrt{3}$,3$\sqrt{3}$].
点评 本题考查正弦定理与余弦定理的应用,三角函数的值的求法,以及三角函数恒等变换的应用,考查计算能力和转化思想,属于中档题.

 53随堂测系列答案
53随堂测系列答案| A. | 5 | B. | 3 | C. | 2 | D. | 1 |
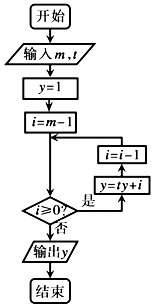
| A. | 61 | B. | 62 | C. | 183 | D. | 184 |