题目内容
已知a＞b＞c，且
+
+
≥0恒成立，则实数k的最大值为（ ）
| 9 |
| a-b |
| 1 |
| b-c |
| k |
| c-a |
分析：由已知，可得出k≤(a-c)(
+
)，利用基本不等式求出(a-c)(
+
)的最值后，只须k≤(a-c)(
+
)的最小值即可，从而再研究a的最大值．
| 9 |
| a-b |
| 1 |
| b-c |
| 9 |
| a-b |
| 1 |
| b-c |
| 9 |
| a-b |
| 1 |
| b-c |
解答：解：a＞b＞c，且
+
+
≥0恒成立，
∴
≤
+
，
两边同乘以a-c得，k≤(a-c)(
+
)，
又(a-c)(
+
)=(a-b+b-c)(
+
)=10+
+
≥10+2
=16．
∴k≤16．
则实数k的最大值为16．
故选B．
| 9 |
| a-b |
| 1 |
| b-c |
| k |
| c-a |
∴
| k |
| a-c |
| 9 |
| a-b |
| 1 |
| b-c |
两边同乘以a-c得，k≤(a-c)(
| 9 |
| a-b |
| 1 |
| b-c |
又(a-c)(
| 9 |
| a-b |
| 1 |
| b-c |
| 9 |
| a-b |
| 1 |
| b-c |
| 9(b-c) |
| a-b |
| a-b |
| b-c |
|
∴k≤16．
则实数k的最大值为16．
故选B．
点评：本题考查参数分离法、基本不等式求最值．考查了转化、变形、配凑常数的方法．
练习册系列答案
尖子生新课堂课时作业系列答案
英才计划同步课时高效训练系列答案
相关题目
，且a＋b＋c＝1，求证：
≥9．
≥9．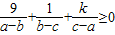
恒成立，则实数k的最大值为（ ）