题目内容
已知椭圆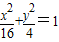
及点M（0，3），求点M到椭圆上点距离的最大值．
【答案】分析：设椭圆上点P的坐标，代入椭圆方程，利用M（0，3）及两点间的距离公式求|PM|的表达式，结合y的范围利用二次函数的性质，即可求出|PM|的最大值．
解答：解：设椭圆上点P的坐标为P（x，y），
则x，y满足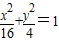
，化简得x2=16-4y2，
根据两点间的距离公式，
∴|PM|=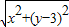
=
=
，
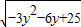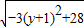∵P（x，y）在椭圆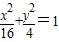
上，∴y∈[-2，2]，
∴当y=-1时，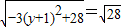
，
∴|PM|≤2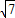
．
故|PM|的最大值是2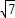
．
点评：本题主要考查了椭圆的方程，以及椭圆的简单性质，属于基础题．
解答：解：设椭圆上点P的坐标为P（x，y），
则x，y满足
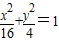，化简得x2=16-4y2，根据两点间的距离公式，
∴|PM|=
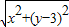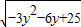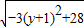==，∵P（x，y）在椭圆
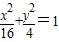上，∴y∈[-2，2]，∴当y=-1时，
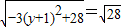，∴|PM|≤2
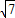．故|PM|的最大值是2
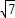．点评：本题主要考查了椭圆的方程，以及椭圆的简单性质，属于基础题．
练习册系列答案
相关题目
已知椭圆
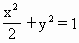及点B(0，－2)，过点B作直线m与椭圆交于C、D两点，
(a＞b＞0)上的点M(1，
)到它的两焦点F1、F2的距离之和为4，A、B分别是它的左顶点和上顶点．
(a＞b＞0)的一个焦点与抛物线y2＝
的焦点F重合，且椭圆短轴的两个端点与F构成正三角形．
恒为定值?若存在，求出E的坐标及定值；若不存在，请说明理由．