题目内容
函数f(x)=a2x-ax+b x∈[-1,2],若f (0)=1,f (1)= ,求
,求
(1)f (x)的解析式
(2)f (x)的值域
(3)f (x)的单调区间.
解:(1)f(x)=a2x-ax+b,x∈[-1,2]
因为f(0)=1,f(1)=
则 (2分)
(2分)
∴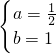
∴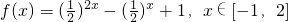 (4分)
(4分)
(2)设t= ,t∈[
,t∈[ ,2].
,2].
∴y=t2-t+1=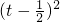 +
+ .
.
∴当t= 时,ymin=
时,ymin= ;
;
当t=2时,ymax=3.
∴函数的值域为:[ ,3].
,3].
(3)令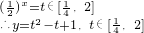 .
.
由于 为单调递减函数
为单调递减函数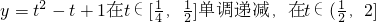 单调递增(12分)
单调递增(12分)
∴ (14分)
(14分)
分析:(1)直接根据f (0)=1以及f (1)= ,列出关于a,b的两个方程,解方程求出a,b即可求f (x)的解析式;
,列出关于a,b的两个方程,解方程求出a,b即可求f (x)的解析式;
(2)令t= ,求出t的取值范围,把问题转化为二次函数在闭区间上求值域的问题,比较对称轴和区间的位置关系即可得出结论;
,求出t的取值范围,把问题转化为二次函数在闭区间上求值域的问题,比较对称轴和区间的位置关系即可得出结论;
(3)令t= ,求出t的取值范围,根据二次函数单调性的求法,再结合复合函数的单调性中的同增异减的性质即可得出结论.
,求出t的取值范围,根据二次函数单调性的求法,再结合复合函数的单调性中的同增异减的性质即可得出结论.
点评:本题是对指数函数知识以及二次函数知识的综合考查.其中涉及到了复合函数的单调性,复合函数的单调性遵循原则是:两个函数单调性相同,复合函数为增函数;两个函数单调性相反,复合函数为减函数;简单的记法就是“同则增,异则减“.
因为f(0)=1,f(1)=

则
 (2分)
(2分)∴
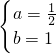
∴
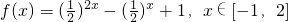 (4分)
(4分)(2)设t=
 ,t∈[
,t∈[ ,2].
,2].∴y=t2-t+1=
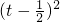 +
+ .
.∴当t=
 时,ymin=
时,ymin= ;
;当t=2时,ymax=3.
∴函数的值域为:[
 ,3].
,3].(3)令
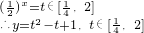 .
.由于
 为单调递减函数
为单调递减函数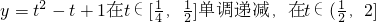 单调递增(12分)
单调递增(12分)∴
 (14分)
(14分)分析:(1)直接根据f (0)=1以及f (1)=
 ,列出关于a,b的两个方程,解方程求出a,b即可求f (x)的解析式;
,列出关于a,b的两个方程,解方程求出a,b即可求f (x)的解析式;(2)令t=
 ,求出t的取值范围,把问题转化为二次函数在闭区间上求值域的问题,比较对称轴和区间的位置关系即可得出结论;
,求出t的取值范围,把问题转化为二次函数在闭区间上求值域的问题,比较对称轴和区间的位置关系即可得出结论;(3)令t=
 ,求出t的取值范围,根据二次函数单调性的求法,再结合复合函数的单调性中的同增异减的性质即可得出结论.
,求出t的取值范围,根据二次函数单调性的求法,再结合复合函数的单调性中的同增异减的性质即可得出结论.点评:本题是对指数函数知识以及二次函数知识的综合考查.其中涉及到了复合函数的单调性,复合函数的单调性遵循原则是:两个函数单调性相同,复合函数为增函数;两个函数单调性相反,复合函数为减函数;简单的记法就是“同则增,异则减“.

练习册系列答案
相关题目