题目内容

定义函数fn(x)=(1+x)n-1,x＞-2,n∈N*.

(1)求证：fn(x)≥nx.

(2)是否存在区间［a,0］(a＜0),使函数n(x)=f3(x)-f2(x)在区间［a,0］上的值域为［ka,0］?若存在，求出最小的k值及相应的区间［a,0］;若不存在，说明理由.

解：（1）证明：fn(x)-nx=(1+x)n-1-nx,

    令g(x)=(1+x)n-1-nx,则g′(x)=n［(1+x)n-1-1］,

    当x∈(-2,0)时，g′(x)＜0;

    当x∈(0,+∞)时,g′x＞0.

∴g(x)在x=0处取得极小值g(0)=0,同时g(x)是学峰函数，则g(0)也是最小值，∴g(x)≥0.

    即fn(x)≥nx(当且仅当x=0取等号).

（2）h(x)=f3(x)=f2(x)=x(1+x)2,

h′(x)=(1+x)2+x·2(1+x)=(1+x)(1+3x),

    令h′(x)=0,得x=-1,x=-∴当x∈(-2,-1)时，h′(x)＞0；当x∈(-1,-)时，h′(x)＜0;

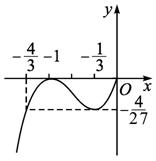
    当x∈(-,+∞)时，h′(x)＞0,故h(x)的草图如图所示：

①在-≤a＜0时，h(x)最小值h(a)=ka.∴k=(1+a)2≥,

②在-≤a≤-时,h(x)最小值=h(-)=-=ka,k=-,≤k≤;

③在a≤-时,h(x)最小值=h(a)=a(1+a)2=ka,k=(1+a)2≥,a=-取等号.

    综上k的最小值为,此时［a,0］=［-,0］.

练习册系列答案
相关题目
假设实数a1，a2，a3，a4是一个等差数列﹐且满足0＜a1＜2及a3=4，若定义函数fn(x)=anx，其中n=1，2，3，4，则下列命题中错误的是（　　）
定义函数fn(x)=(1+x)n-1(x＞-2，n∈N*)其导函数记为
f
′
n
(x)．
（Ⅰ）求y=fn（x）-nx的单调递增区间；
（Ⅱ）若
f
′
n
(x0)
f
′
n+1
(x0)
=
fn(1)
fn+1(1)
，求证：0＜x0＜1；
（Ⅲ）设函数φ（x）=f3（x）-f2（x），数列{ak}前k项和为Sk，2kSk=φ（k-1）+2kak，其中a1=1．对于给定的正整数n（n≥2），数列{bn}满足ak+1bk+1=（k-n）bk（k=1，2…，n-1），且b1=1，求b1+b2+…+bn．
（2012•香洲区模拟）定义函数fn(x)=(1+x)n-1，x＞-2，n∈N
（1）求f3（x）的极值点；
（1）求证：fn（x）≥nx；
（2）是否存在区间[a，0]（a＜0），使函数h（x）=f3（x）-f2（x）在区间[a，0]上的值域为[k-a，0]？若存在，求出最小的k值及相应的区间[a，0]，若不存在，说明理由．
定义函数fn(x)=(1+x)n-1，x＞-2(n∈N*)，其导函数为fn′(x)．

(1)求证fn(x)≥nx；

(2)设，求证0＜x0＜1；

(3)是否存在区间[a，b)(-∞，0]，使函数h(x)=f3(x)-f2(x)在区间[a，b)的值域为[ka，kb]?若存在，求出最小的A的值及相应的区间[a，b]．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网