题目内容
(2012•香洲区模拟)定义函数fn(x)=(1+x)n-1,x>-2,n∈N
(1)求f3(x)的极值点;
(1)求证:fn(x)≥nx;
(2)是否存在区间[a,0](a<0),使函数h(x)=f3(x)-f2(x)在区间[a,0]上的值域为[k-a,0]?若存在,求出最小的k值及相应的区间[a,0],若不存在,说明理由.
(1)求f3(x)的极值点;
(1)求证:fn(x)≥nx;
(2)是否存在区间[a,0](a<0),使函数h(x)=f3(x)-f2(x)在区间[a,0]上的值域为[k-a,0]?若存在,求出最小的k值及相应的区间[a,0],若不存在,说明理由.
分析:(1)由函数f3(x)=(1+x)3-1,知f3′(x)=3(1+x)2,由此能求出f3(x)的极值点.
(2)fn(x)-nx=(1+x)n-1-nx,令g(x)=(1+x)n-1-nx,则g′(x)=n[(1+x)n-1-1].由此利用导数性质能够证明fn(x)≥nx.
(3)由h(x)=f3(x)-f2(x)=x(1+x)2,知h′(x)=(1+x)2+2x(1+x)=(1+x)(1+3x),令h′(x)=0,得x=-1,x=-
.由此利用分类讨论思想能求出知k的最小值及本应的[a,0].
(2)fn(x)-nx=(1+x)n-1-nx,令g(x)=(1+x)n-1-nx,则g′(x)=n[(1+x)n-1-1].由此利用导数性质能够证明fn(x)≥nx.
(3)由h(x)=f3(x)-f2(x)=x(1+x)2,知h′(x)=(1+x)2+2x(1+x)=(1+x)(1+3x),令h′(x)=0,得x=-1,x=-
| 1 |
| 3 |
解答:解:(1)∵函数fn(x)=(1+x)n-1,x>-2,n∈N,
∴f3(x)=(1+x)3-1,
∴f3′(x)=3(1+x)2,
令f3′(x)=0 ,得x=-1,
∵定义域(-2,+∞),∴列表讨论,得:
∴x=-1为极小值点,无极大值点.…(3分)
(2)证明:fn(x)-nx=(1+x)n-1-nx,
令g(x)=(1+x)n-1-nx,
则g′(x)=n[(1+x)n-1-1].
令g′(x)=0,得x=0.…(5分)
当x∈(-2,-1)时,-1<1+x<0,n为奇数时,(1+x)n<1;
当x∈[-1,0)时,0≤+x<1,0<(1+x)n<1,
∴x∈(-2,0)时,(1+x)n<1,故g′(x)=n[(1+x)n-1-1]<0,
函数g(x)单调递减;
而x∈(0,+∞),(1+x)n>1,故g′(x)=n[(1+x)n-1-1]>0,
函数g(x)单调递增;
∴g(x)在x=0处取得最小值g(0)=0.
∴g(x)≥0,即fn(x)≥nx.(当且仅当x=0时取等号).…10
(3)h(x)=f3(x)-f2(x)=x(1+x)2,
h′(x)=(1+x)2+2x(1+x)=(1+x)(1+3x),
令h′(x)=0,得x=-1,x=-
.
∴当x∈(-2,-1)时,h′(x)>0;
当x∈(-1,-
)时,h′(x)<0;
当x∈(-
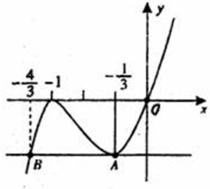
,+∞)时,h′(x)>0.故h(x)的草图如图所示.
在-
≤a<0时,h(x)min=h(a)=ka,∴k=(1+a)2≥
.
②在-
≤a≤-
时,h(x)min=h(-
)=-
=ka,y=-
,
≤k≤
,
③在a≤-
时,h(x)min=h(a)=a(1+a)2=ka.
∴k=(1+a)2≥
,a=-
时取等号.
综上讨论可知k的最小值为
,此时[a,0]=[-
,0].…(14分)
∴f3(x)=(1+x)3-1,
∴f3′(x)=3(1+x)2,
令f3′(x)=0 ,得x=-1,
∵定义域(-2,+∞),∴列表讨论,得:
| x | (-2,-1) | -1 | (-1,+∞) |
| f′(x) | - | 0 | + |
| f(x) | 递减 | 极小值 | 递增 |
(2)证明:fn(x)-nx=(1+x)n-1-nx,
令g(x)=(1+x)n-1-nx,
则g′(x)=n[(1+x)n-1-1].
令g′(x)=0,得x=0.…(5分)
当x∈(-2,-1)时,-1<1+x<0,n为奇数时,(1+x)n<1;
当x∈[-1,0)时,0≤+x<1,0<(1+x)n<1,
∴x∈(-2,0)时,(1+x)n<1,故g′(x)=n[(1+x)n-1-1]<0,
函数g(x)单调递减;
而x∈(0,+∞),(1+x)n>1,故g′(x)=n[(1+x)n-1-1]>0,
函数g(x)单调递增;
∴g(x)在x=0处取得最小值g(0)=0.
∴g(x)≥0,即fn(x)≥nx.(当且仅当x=0时取等号).…10
(3)h(x)=f3(x)-f2(x)=x(1+x)2,

h′(x)=(1+x)2+2x(1+x)=(1+x)(1+3x),
令h′(x)=0,得x=-1,x=-
| 1 |
| 3 |
∴当x∈(-2,-1)时,h′(x)>0;
当x∈(-1,-
| 1 |
| 3 |
当x∈(-
| 1 |
| 3 |
在-
| 1 |
| 3 |
| 4 |
| 9 |
②在-
| 4 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 4 |
| 27 |
| 4 |
| 27a |
| 1 |
| 9 |
| 4 |
| 9 |
③在a≤-
| 4 |
| 3 |
∴k=(1+a)2≥
| 1 |
| 9 |
| 4 |
| 3 |
综上讨论可知k的最小值为
| 1 |
| 9 |
| 4 |
| 3 |
点评:本题考查函数的极值点的求法,考查不等式的证明,考查最小值的求法.综合性强,难度大,具有一定的探索性,对数学思维的要求较高.解题时要认真审题,注意构造法的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

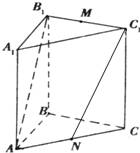 (2012•香洲区模拟)如图,直三棱柱ABC-A1B1C1中,∠ABC=90°,AB=4,BC=4,BB1=3,M、N分别是B1C1和AC的中点.
(2012•香洲区模拟)如图,直三棱柱ABC-A1B1C1中,∠ABC=90°,AB=4,BC=4,BB1=3,M、N分别是B1C1和AC的中点.