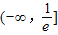题目内容

若?x∈R，使aex≤x（e是自然对数的底数），则a的取值范围是（　　）
分析：转化aex≤x，为a的不等式，求出表达式的最小值，即可得到a的取值范围．
解答：解：aex≤x（e是自然对数的底数），转化为：a≤
x
ex
，令y=
x
ex
，
则y′=
ex-xex
ex
，令y′=0，可得x=1，当x=1时函数y取得最小值
1
e
，
所以a的取值范围是(-∞，
1
e
]．
故选B．
点评：本题考查函数的导数的最值的应用，考查转化思想与计算能力．
练习册系列答案
相关题目
设a＞0，f（x）=
ex
a
+
a
ex
是R上的偶函数，
（1）求a的值；
（2）若x∈（0，+∞）时，此时函数f（x）的图象上是否存在两点，使这两点的连线与轴平行？并说明理由．
设a＞0，f（x）=
ex
a
+
a
ex
是R上的偶函数，
（1）求a的值；
（2）若x∈（0，+∞）时，此时函数f（x）的图象上是否存在在两点，使这两点的连线与轴平行？并说明理由．
若?x∈R，使aex≤x（e是自然对数的底数），则a的取值范围是（　　）
A．（-∞，0]B．(-∞，
1
e
]		C．（-∞，1]D．（-∞，e]
若?x∈R，使aex≤x（e是自然对数的底数），则a的取值范围是（ ）
A．（-∞，0]
B．
C．（-∞，1]
D．（-∞，e]

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网