题目内容
(本小题满分12分) 在直角坐标系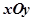 中,以坐标原点
中,以坐标原点 为圆心的圆与直线:
为圆心的圆与直线: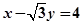 相切.
相切.
(1)求圆 的方程;
的方程;
(2)若圆 上有两点
上有两点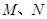 关于直线
关于直线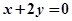 对称,且
对称,且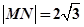 ,求直线MN的方程;
,求直线MN的方程;
(3)圆 与x轴相交于A、B两点,圆内的动点P使|PA|、|PO|、|PB|成等比数列,求
与x轴相交于A、B两点,圆内的动点P使|PA|、|PO|、|PB|成等比数列,求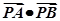 的取值范围.
的取值范围.
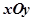 中,以坐标原点
中,以坐标原点 为圆心的圆与直线:
为圆心的圆与直线: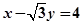 相切.
相切.(1)求圆
 的方程;
的方程;(2)若圆
 上有两点
上有两点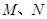 关于直线
关于直线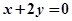 对称,且
对称,且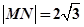 ,求直线MN的方程;
,求直线MN的方程;(3)圆
 与x轴相交于A、B两点,圆内的动点P使|PA|、|PO|、|PB|成等比数列,求
与x轴相交于A、B两点,圆内的动点P使|PA|、|PO|、|PB|成等比数列,求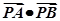 的取值范围.
的取值范围.(1) .(2)
.(2) 或
或 .(3)
.(3) .
.
 .(2)
.(2) 或
或 .(3)
.(3) .
. (1)关键是利用点到直线的距离求出半径.
(2)可设直线MN的方程为 .则圆心
.则圆心 到直线MN的距离
到直线MN的距离 .由垂径分弦定理得:
.由垂径分弦定理得: ,从而解出m的值.
,从而解出m的值.
(3) 不妨设 .由
.由 得
得 .
.
设 ,由
,由 成等比数列,得
成等比数列,得 ,即
,即 .
. =
= ,再根据点P在圆内,确定出y的取值范围,进而确定
,再根据点P在圆内,确定出y的取值范围,进而确定 的取值范围.
的取值范围.
解:(1)依题设,圆 的半径
的半径 等于原点
等于原点 到直线
到直线 的距离,
的距离,
即 .
.
得圆 的方程为
的方程为 . ………………3分
. ………………3分
(2)由题意,可设直线MN的方程为 .
.
则圆心 到直线MN的距离
到直线MN的距离 . ………………4分
. ………………4分
由垂径分弦定理得: ,即
,即 .
.
所以直线MN的方程为: 或
或 .…………6分
.…………6分
(3)不妨设 .由
.由 得
得 .
.
设 ,由
,由 成等比数列,得
成等比数列,得
 ,即
,即 . …………8分
. …………8分
∴ =
=
由于点 在圆
在圆 内,故
内,故 由此得
由此得 . …………10分
. …………10分
所以 的取值范围为
的取值范围为 . ………………12分
. ………………12分
(2)可设直线MN的方程为
 .则圆心
.则圆心 到直线MN的距离
到直线MN的距离 .由垂径分弦定理得:
.由垂径分弦定理得: ,从而解出m的值.
,从而解出m的值.(3) 不妨设
 .由
.由 得
得 .
.设
 ,由
,由 成等比数列,得
成等比数列,得 ,即
,即 .
. =
= ,再根据点P在圆内,确定出y的取值范围,进而确定
,再根据点P在圆内,确定出y的取值范围,进而确定 的取值范围.
的取值范围.解:(1)依题设,圆
 的半径
的半径 等于原点
等于原点 到直线
到直线 的距离,
的距离,即
 .
.得圆
 的方程为
的方程为 . ………………3分
. ………………3分(2)由题意,可设直线MN的方程为
 .
.则圆心
 到直线MN的距离
到直线MN的距离 . ………………4分
. ………………4分由垂径分弦定理得:
 ,即
,即 .
.所以直线MN的方程为:
 或
或 .…………6分
.…………6分(3)不妨设
 .由
.由 得
得 .
.设
 ,由
,由 成等比数列,得
成等比数列,得 ,即
,即 . …………8分
. …………8分∴
 =
=
由于点
 在圆
在圆 内,故
内,故 由此得
由此得 . …………10分
. …………10分所以
 的取值范围为
的取值范围为 . ………………12分
. ………………12分
练习册系列答案
相关题目
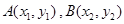 是
是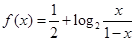 的图象上任意两点,设点
的图象上任意两点,设点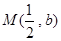 ,且
,且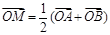 ,若
,若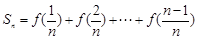 ,其中
,其中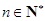 ,且
,且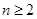 .
.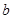 的值;
的值; 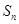 ;
;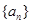 中
中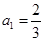 ,当
,当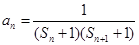 ,设数列
,设数列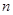 项和为
项和为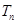 ,求
,求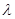 的取值范围使
的取值范围使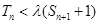 对一切
对一切 ,
, ,其中
,其中 ,
,
 和
和  的值;
的值; 与
与 夹角
夹角 的余弦值.
的余弦值.
 ,
, ,若点M在直线OB上,则
,若点M在直线OB上,则 的最小值为___ _
的最小值为___ _ =(1,2),
=(1,2), =(-2,y),若
=(-2,y),若 ,则
,则 = 。
= 。 是
是 边
边 的中点,过点
的中点,过点 所在直线于
所在直线于 ,若
,若 ,则
,则 .
.  ,
, ,
, ,且
,且 ,则向量
,则向量 与
与 的夹角为( )
的夹角为( )



 满足
满足 ,且
,且 与
与 的夹角为120°,
的夹角为120°, ,则
,则 的取值范围是 .
的取值范围是 .  中,
中, ( )
( )