题目内容
已知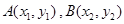 是
是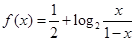 的图象上任意两点,设点
的图象上任意两点,设点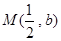 ,且
,且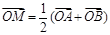 ,若
,若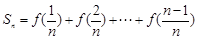 ,其中
,其中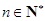 ,且
,且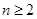 .
.
(1)求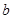 的值;
的值;
(2)求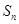 ;
;
(3)数列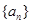 中
中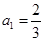 ,当
,当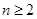 时,
时,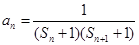 ,设数列
,设数列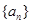 的前
的前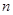 项和为
项和为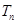 ,求
,求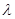 的取值范围使
的取值范围使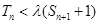 对一切
对一切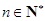 都成立.
都成立.
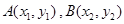 是
是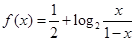 的图象上任意两点,设点
的图象上任意两点,设点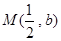 ,且
,且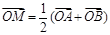 ,若
,若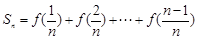 ,其中
,其中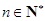 ,且
,且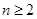 .
.(1)求
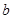 的值;
的值; (2)求
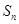 ;
;(3)数列
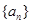 中
中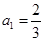 ,当
,当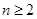 时,
时,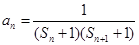 ,设数列
,设数列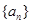 的前
的前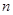 项和为
项和为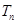 ,求
,求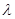 的取值范围使
的取值范围使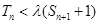 对一切
对一切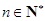 都成立.
都成立.(1)由 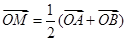 ,得点
,得点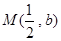 是
是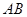 的中点,
的中点,
则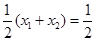 , 故
, 故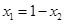 ,
,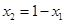 ,
,
所以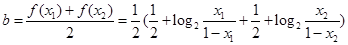

(2)由(1)知当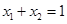 时,
时,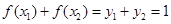 .
.
又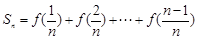 ,∴
,∴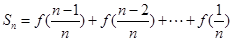 ,
,
∴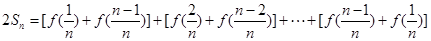

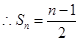 (
(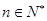 ,且
,且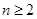 ).
).
(3)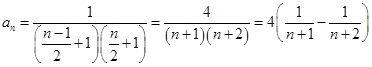 ,
,
故当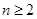 时
时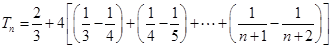
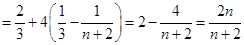 ,故由
,故由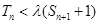 得
得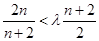 ,
,
即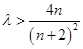 ,只要
,只要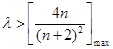 ,
,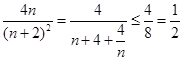 ,
,
故当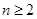 时,
时,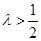 ;当
;当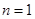 是
是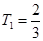 ,
,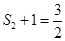 ,由
,由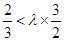 得
得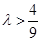 ,而
,而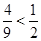 .
.
故当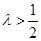 时可以对一切
时可以对一切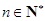 不等式
不等式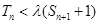 都成立.
都成立.
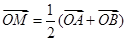 ,得点
,得点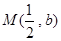 是
是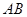 的中点,
的中点,则
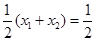 , 故
, 故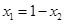 ,
,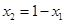 ,
, 所以
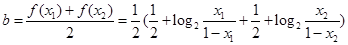

(2)由(1)知当
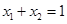 时,
时,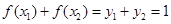 .
. 又
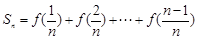 ,∴
,∴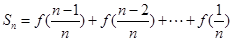 ,
,∴
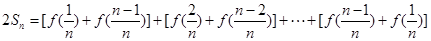

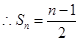 (
(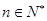 ,且
,且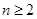 ).
).(3)
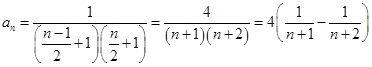 ,
,故当
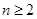 时
时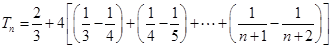
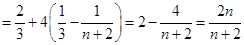 ,故由
,故由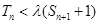 得
得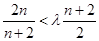 ,
,即
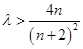 ,只要
,只要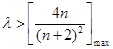 ,
,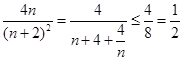 ,
,故当
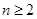 时,
时,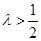 ;当
;当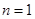 是
是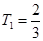 ,
,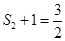 ,由
,由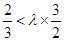 得
得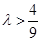 ,而
,而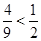 .
.故当
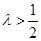 时可以对一切
时可以对一切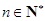 不等式
不等式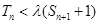 都成立.
都成立.
|
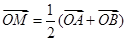 ,得点
,得点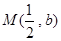 是
是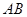 的中点,则
的中点,则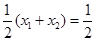 , 故
, 故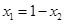 ,
,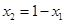 .这是解本小题的关键.
.这是解本小题的关键.(2) 由(1)知当
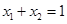 时,
时,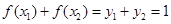 .
. 又
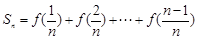 ,下面采用倒序相加的方法求和即可.
,下面采用倒序相加的方法求和即可.(3)
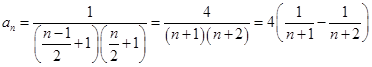
所以采用裂项求和的方法求解即可.
【点评】数列是以正整数为自变量的函数,从函数入手设计数列试题是自然的.本题从函数图象的对称性出发构造了一个函数值的数列,再从这些已经解决的问题入手构造了一个裂项求和问题和一个不等式恒成立问题,试题设计逐步深入.解答数列求和时要注意起首项是不是可以融入整体,实际上本题得到的
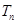 对
对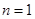 也成立
也成立
练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
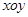 中,若
中,若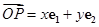 (其中
(其中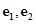 分别是斜坐标系中的
分别是斜坐标系中的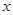 轴和
轴和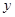 轴正方向上的单位向量,
轴正方向上的单位向量,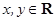 ,
,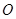 为坐标原点),则称有序数对
为坐标原点),则称有序数对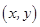 为点
为点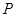 的斜坐标.在平面斜坐标系
的斜坐标.在平面斜坐标系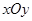 中,若点
中,若点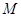 的斜坐标为(1,2),点
的斜坐标为(1,2),点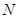 的斜坐标为(3,4),且
的斜坐标为(3,4),且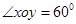 ,则
,则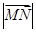 等于 ( )
等于 ( ) 
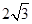
 ,
, ,若直线
,若直线 上存在点
上存在点 满足
满足 ,则实数
,则实数 的取值范围是( )
的取值范围是( )



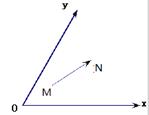
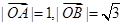 ,
,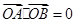 点
点 在
在 内,且
内,且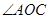
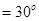 。设
。设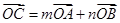
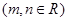 ,则
,则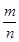 等于
等于


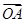 ,
,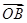 的夹角为60°,|
的夹角为60°,|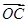 =2
=2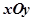 中,以坐标原点
中,以坐标原点 为圆心的圆与直线:
为圆心的圆与直线: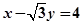 相切.
相切.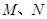 关于直线
关于直线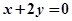 对称,且
对称,且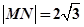 ,求直线MN的方程;
,求直线MN的方程;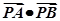 的取值范围.
的取值范围. 的夹角为
的夹角为 ,
, ,则向量
,则向量 的模( )
的模( )  与
与 的夹角为
的夹角为 ,且
,且 ,则
,则 等于
等于