题目内容

A、B、C是球面上三点,已知弦AB=18 cm,BC=24 cm,AC=30 cm,平面ABC与球心的距离恰好为球半径的一半,求球的表面积.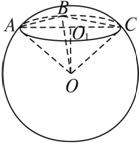

思路解析:求球的表面积就是求球的半径、本例求球的半径R的方法是列出R的方程、由方程解得R.

解:∵AB2+BC2=AC2,

∴△ABC是直角三角形.∴△ABC的外接圆圆心O1在AC的中点上.

过A、B、C三点的平面截球O得圆O1的半径为R=15 cm.

在Rt△OO1C中,R2=()2+r2,∴R2=+152.∴R2=300.

∴S球=4πR2=1 200π(cm2).

练习册系列答案
相关题目
（2010•成都一模）如图，设A、B、C是球O面上的三点，我们把大圆的劣弧
BC
、
CA
、
AB
在球面上围成的部分叫做球面三角形，记作球面三角形ABC，在球面三角形ABC中，OA=1，设
BC
=a，
CA
=b，
AB
=c，a，b．c∈(0，π)，二面角B-OA-C、
C-OB-A、A-OC-B的大小分别为α、β、γ，给出下列命题：
①若α=β=γ=
π
2
，则球面三角形ABC的面积为
π
2
；
②若a=b=c=
π
3
，则四面体OABC的侧面积为
π
2
；
③圆弧
AB
在点A处的切线l1与圆弧
CA
在点A处的切线l2的夹角等于a；
④若a=b，则α=β．
其中你认为正确的所有命题的序号是
①②④
①②④
．

已知A、B、C是球O面上的三点，则下列命题中，真命题的个数是

①若AB＝6，AC＝8，BC＝10，OA＝10，则O到平面ABC的距离是5

②若∠BAC＝90°，E是BC中点，AE＝4，OE＝3，则OA＝5

③若∠BAC＝60°，BC＝4，OB＝，则O到平面ABC的距离是

④若E是△ABC的BC边上的中点且OE⊥平面ABC，则△ABC不一定是直角三角形

[　　]

A．1

B．2

C．3

D．4
如图，设A、B、C是球O面上的三点，我们把大圆的劣弧在球面上围成的部分叫做球面三角形，记作球面三角形ABC，在球面三角形ABC中，OA=1，设，二面角B-OA-C、
C-OB-A、A-OC-B的大小分别为α、β、γ，给出下列命题：
①若，则球面三角形ABC的面积为；
②若，则四面体OABC的侧面积为；
③圆弧在点A处的切线l1与圆弧在点A处的切线l2的夹角等于a；
④若a=b，则α=β．
其中你认为正确的所有命题的序号是    ．
如图，设A、B、C是球O面上的三点，我们把大圆的劣弧在球面上围成的部分叫做球面三角形，记作球面三角形ABC，在球面三角形ABC中，OA=1，设，二面角B-OA-C、
C-OB-A、A-OC-B的大小分别为α、β、γ，给出下列命题：
①若，则球面三角形ABC的面积为；
②若，则四面体OABC的侧面积为；
③圆弧在点A处的切线l1与圆弧在点A处的切线l2的夹角等于a；
④若a=b，则α=β．
其中你认为正确的所有命题的序号是    ．
如图，设A、B、C是球O面上的三点，我们把大圆的劣弧在球面上围成的部分叫做球面三角形，记作球面三角形ABC，在球面三角形ABC中，OA=1，设，二面角B-OA-C、
C-OB-A、A-OC-B的大小分别为α、β、γ，给出下列命题：
①若，则球面三角形ABC的面积为；
②若，则四面体OABC的侧面积为；
③圆弧在点A处的切线l1与圆弧在点A处的切线l2的夹角等于a；
④若a=b，则α=β．
其中你认为正确的所有命题的序号是    ．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网