题目内容
【题目】选修4-4：坐标系与参数方程
在平面直角坐标系中，以原点为极点，以
轴的非负半轴为极轴且取相同的单位长度建立极坐标系，曲线
的极坐标方程为：
.
（1）若曲线
的参数方程为
（
为参数），求曲线的直角坐标方程和曲线的普通方程；
（2）若曲线的参数方程为（
为参数），
，且曲线与曲线的交点分别为
、
，求
的取值范围.
【答案】（1）曲线
的直角坐标方程为： 
曲线
的普通方程为：
.
(2) 
【解析】
分析：第一问首先应用极坐标与平面直角坐标的转换关系，求得曲线
的直角坐标方程，
之后对曲线
的参数方程进行消参，求得其普通方程；第二问将曲线的参数方程代入的方程，得到关于
的关系式，利用韦达定理求得两个和与两根积的值，之后应用参数的几何意义以及题中所求得的范围，最后借助于对三角函数值域的求解求得结果.
详解：（1）
曲线的直角坐标方程为： 
曲线的普通方程为：
（2）将的参数方程：
代入的方程：
得：
由
的几何意义可得：
【题目】某企业2018年招聘员工，其中
，
，
，
，
五种岗位的应聘人数、录用人数和录用比例（精确到1%）如下：
岗位 | 男性 应聘人数 | 男性 录用人数 | 男性 录用比例 | 女性 应聘人数 | 女性 录用人数 | 女性 录用比例 |
| 269 | 167 |
| 40 | 24 |
|
| 40 | 12 |
| 202 | 62 |
|
| 177 | 57 |
| 184 | 59 |
|
| 44 | 26 |
| 38 | 22 |
|
| 3 | 2 |
| 3 | 2 |
|
总计 | 533 | 264 |
| 467 | 169 |
|
（1）从表中所有应聘人员中随机选择1人，试估计此人被录用的概率；
（2）从应聘岗位的6人中随机选择2人.记
为这2人中被录用的人数，求的分布列和数学期望；
（3）表中，，，，各岗位的男性、女性录用比例都接近（二者之差的绝对值不大于
），但男性的总录用比例却明显高于女性的总录用比例.研究发现，若只考虑其中某四种岗位，则男性、女性的总录用比例也接近，请写出这四种岗位.（只需写出结论）
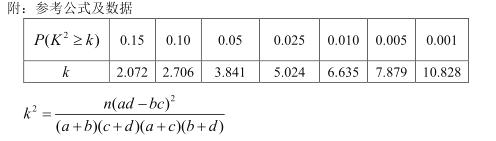
【题目】共享单车已成为一种时髦的新型环保交通工具，某共享单车公司为了拓展市场，对
两个品牌的共享单车在编号分别为
的五个城市的用户人数（单位：十万）进行统计，得到数据如下：
城市 品牌 | 1 | 2 | 3 | 4 | 5 |
A品牌 | 3 | 4 | 12 | 6 | 8 |
B品牌 | 4 | 3 | 7 | 9 | 5 |
（Ⅰ）若共享单车用户人数超过50万的城市称为“优城”，否则称为“非优城”，据此判断能否有85%的把握认为“优城”和共享单车品牌有关？
（Ⅱ）若不考虑其它因素，为了拓展市场，对A品牌要从这五个城市选择三个城市进行宣传，
（ⅰ）求城市2被选中的概率；
（ⅱ）求在城市2被选中的条件下城市3也被选中的概率．
