题目内容
【题目】已知函数f(x)= ![]() sin
sin ![]() cos
cos ![]() +sin2
+sin2 ![]() (ω>0,0<φ<
(ω>0,0<φ< ![]() ).其图象的两个相邻对称中心的距离为
).其图象的两个相邻对称中心的距离为 ![]() ,且过点(
,且过点( ![]() ,1).
,1).
(1)函数f(x)的解析式;
(2)在△ABC中,角A,B,C所对的边分别为a,b,c.已知 ![]() =
= ![]() .且f(A)=
.且f(A)= ![]() ,求角C的大小.
,求角C的大小.
【答案】
(1)解:由题意得,f(x)= ![]() sin(ωx+φ)+
sin(ωx+φ)+ ![]() [1﹣cos(ωx+φ)]
[1﹣cos(ωx+φ)]
= ![]() ,
,
∵两个相邻对称中心的距离为 ![]() ,则T=π,
,则T=π,
∴ ![]() ,且ω>0,解得ω=2,
,且ω>0,解得ω=2,
又f(x)过点 ![]() ,∴
,∴ ![]() ,
,
则 ![]() ,即cosφ=
,即cosφ= ![]() ,由0<φ<
,由0<φ< ![]() 得,φ=
得,φ= ![]() ,
,
∴f(x)= ![]() ;
;
(2)解:在△ABC中,由余弦定理得b2=a2+c2﹣2accosB,
∴b2﹣a2﹣c2=﹣2accosB,
同理可得,c2﹣a2﹣b2=﹣2abcosC,
代入 ![]() 得,
得, ![]() =
= ![]() ,
,
由正弦定理得, ![]() ,
,
由0<C<π得sinC≠0,∴sinBcosC=2sinAcosB﹣sinCcosB,
∴2sinAcosB=sinBcosC+sinCcosB=sin(B+C)=sinA,
由0<A<π得sinA≠0,化简得cosB= ![]() ,
,
∵0<B<π,∴B= ![]() ,
,
由 ![]() 得
得 ![]() ,则
,则 ![]() ,
,
∵ ![]() ,∴
,∴ ![]() ,则
,则 ![]() 或
或 ![]() ,
,
解得 ![]() 或
或 ![]() ,
,
所以当 ![]() 时,
时, ![]() ;当
;当 ![]() 时,
时, ![]()
【解析】(1)根据二倍角公式、两角差的正弦公式化简解析式,结合条件求出周期,由周期公式求出ω,将点 ![]() 代入解析式化简后,由内角的范围和特殊角的三角函数值求出φ,即可求出f(x);(2)由正弦定理和余弦定理化简已知的式子,利用两角和的正弦公式和内角的范围求出B,由解析式化简
代入解析式化简后,由内角的范围和特殊角的三角函数值求出φ,即可求出f(x);(2)由正弦定理和余弦定理化简已知的式子,利用两角和的正弦公式和内角的范围求出B,由解析式化简 ![]() ,根据角A的范围和特殊角的三角函数值求出A,再由内角和定理求出C.
,根据角A的范围和特殊角的三角函数值求出A,再由内角和定理求出C.
【考点精析】根据题目的已知条件,利用正弦定理的定义的相关知识可以得到问题的答案,需要掌握正弦定理:![]() .
.

【题目】下表提供了某厂节能降耗技术改造后生产产品过程中记录的产量x(吨)与相应的生产能耗y(吨)标准煤的几组对照数据:
x | 3 | 4 | 5 | 6 |
y | 2.5 | 3 | 4 | 4.5 |
(1)求y关于x的线性回归方程;(已知 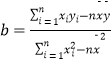 )
)
(2)已知该厂技术改造前100吨甲产品能耗为90吨标准煤,试根据(1)求出的线性回归方程,预测生产100吨甲产品的生产能耗比技术改造前降低了多少吨标准煤.