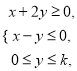题目内容
【题目】如图所示,正三角形![]() 所在平面与梯形
所在平面与梯形![]() 所在平面垂直,
所在平面垂直, ![]() ,
, ![]() ,
, ![]() 为棱
为棱![]() 的中点.
的中点.
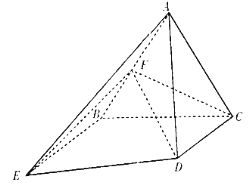
(1)求证: ![]() 平面
平面![]() ;
;
(2)若直线![]() 与平面
与平面![]() 所成的角为30°,求三棱锥
所成的角为30°,求三棱锥![]() 的体积.
的体积.
【答案】(1)见解析;(2) ![]() .
.
【解析】试题分析:(1)先根据面面垂直性质定理转化为线面垂直![]() 平面
平面![]() ,,再利用线面垂直性质定理得线线垂直
,,再利用线面垂直性质定理得线线垂直![]() ,由正三角形性质得
,由正三角形性质得![]() ,最后根据线面垂直判定定理得结论,(2)先根据线面垂直
,最后根据线面垂直判定定理得结论,(2)先根据线面垂直![]() 平面
平面![]() 确定直线
确定直线![]() 与平面
与平面![]() 所成的角的平面角为
所成的角的平面角为![]() ,求出点
,求出点![]() 到平面
到平面![]() 的距离,根据
的距离,根据![]() 为
为![]() 的中点,可得点
的中点,可得点![]() 到平面
到平面![]() 的距离为点
的距离为点![]() 到平面
到平面![]() 的距离一半,利用锥体体积公式可得
的距离一半,利用锥体体积公式可得![]() ,再根据等体积法可得
,再根据等体积法可得![]() .
.
试题解析:(1)∵平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,
且![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() ,
,
∴![]() ,
,
又∵![]() 为正三角形,
为正三角形, ![]() 为
为![]() 的中点,
的中点,
∴![]() ,
,
又∵![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() ;
;
(2)取![]() 中点
中点![]() ,连接
,连接![]() ,
,
易知![]() 平面
平面![]() ,∴
,∴![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,
,
∵![]() 中,
中, ![]() ,∴
,∴![]() ,
,
∵![]() 为正三角形,
为正三角形, ![]() 为
为![]() 的中点,
的中点,
∴![]() 且
且![]() ,
,
∵平面![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() ,
,
又∵![]() 为
为![]() 的中点,∴点
的中点,∴点![]() 到平面
到平面![]() 的距离为
的距离为![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() .
.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目