题目内容
已知椭圆方程为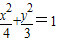 ,试确定m的范围,使得椭圆上有不同的两点关于直线y=4x+m对称.
,试确定m的范围,使得椭圆上有不同的两点关于直线y=4x+m对称.
【答案】分析:根据对称性可知线段AB被直线y=4x+m垂直平分,从而可得直线AB的斜率k=- ,直线AB与椭圆有两个交点,且AB的中点M在直线y=4x+m,可设直线AB 的方程为y=
,直线AB与椭圆有两个交点,且AB的中点M在直线y=4x+m,可设直线AB 的方程为y=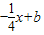 ,联立方程
,联立方程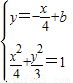 整理可得13x2-8bx+16(b2-3)=0可求中点M,由△=64b2-4×13×16(b2-3)>0可求b的范围,由中点M在直线y=4x+m可得m,b 的关系,从而可求m的范围
整理可得13x2-8bx+16(b2-3)=0可求中点M,由△=64b2-4×13×16(b2-3)>0可求b的范围,由中点M在直线y=4x+m可得m,b 的关系,从而可求m的范围
解答:解:设椭圆上关于直线y=4x+m对称的点A(x1,y1),B(x2,y2),
则根据对称性可知线段AB被直线y=4x+m垂直平分.
可得直线AB的斜率k=- ,直线AB与椭圆有两个交点,且AB的中点M(x,y)在直线y=4x+m,
,直线AB与椭圆有两个交点,且AB的中点M(x,y)在直线y=4x+m,
故可设直线AB 的方程为y=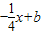 ,
,
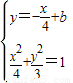 整理可得13x2-8bx+16(b2-3)=0,
整理可得13x2-8bx+16(b2-3)=0,
所以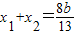 ,
,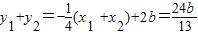 ,
,
由△=64b2-4×13×16(b2-3)>0可得,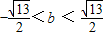
所以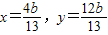 代入直线y=4x+m可得m=
代入直线y=4x+m可得m=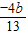
所以,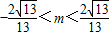 .
.
点评:本题主要考查了直线与椭圆的位置关系的应用,解题的关键是灵活应用已知中的对称性设出直线方程,且由中点在y=4x+m上建立m,b之间的关系,还要注意方程的根与系数的关系的应用.
 ,直线AB与椭圆有两个交点,且AB的中点M在直线y=4x+m,可设直线AB 的方程为y=
,直线AB与椭圆有两个交点,且AB的中点M在直线y=4x+m,可设直线AB 的方程为y=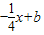 ,联立方程
,联立方程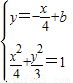 整理可得13x2-8bx+16(b2-3)=0可求中点M,由△=64b2-4×13×16(b2-3)>0可求b的范围,由中点M在直线y=4x+m可得m,b 的关系,从而可求m的范围
整理可得13x2-8bx+16(b2-3)=0可求中点M,由△=64b2-4×13×16(b2-3)>0可求b的范围,由中点M在直线y=4x+m可得m,b 的关系,从而可求m的范围解答:解:设椭圆上关于直线y=4x+m对称的点A(x1,y1),B(x2,y2),
则根据对称性可知线段AB被直线y=4x+m垂直平分.
可得直线AB的斜率k=-
 ,直线AB与椭圆有两个交点,且AB的中点M(x,y)在直线y=4x+m,
,直线AB与椭圆有两个交点,且AB的中点M(x,y)在直线y=4x+m,故可设直线AB 的方程为y=
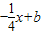 ,
,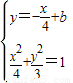 整理可得13x2-8bx+16(b2-3)=0,
整理可得13x2-8bx+16(b2-3)=0,所以
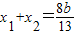 ,
,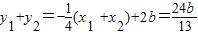 ,
,由△=64b2-4×13×16(b2-3)>0可得,
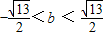
所以
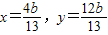 代入直线y=4x+m可得m=
代入直线y=4x+m可得m=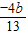
所以,
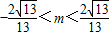 .
.点评:本题主要考查了直线与椭圆的位置关系的应用,解题的关键是灵活应用已知中的对称性设出直线方程,且由中点在y=4x+m上建立m,b之间的关系,还要注意方程的根与系数的关系的应用.

练习册系列答案
 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
 已知椭圆C:
已知椭圆C: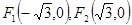 ,离心率是
,离心率是 。椭圆C的左,右顶点分别记为A,B。点S是椭圆C上位于
。椭圆C的左,右顶点分别记为A,B。点S是椭圆C上位于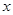 轴上方的动点,直线AS,BS与直线
轴上方的动点,直线AS,BS与直线 分别交于M,N两点。
分别交于M,N两点。 .
. 与双曲线
与双曲线 -y2=1有公共焦点,且离心率为
-y2=1有公共焦点,且离心率为 .A,B分别是椭圆C的左顶点和右顶点.点S是椭圆C上位于x轴上方的动点.直线AS,BS分别与直线l:x=
.A,B分别是椭圆C的左顶点和右顶点.点S是椭圆C上位于x轴上方的动点.直线AS,BS分别与直线l:x= 分别交于M,N两点.
分别交于M,N两点. ?若存在确定点T的个数,若不存在,说明理由.
?若存在确定点T的个数,若不存在,说明理由.