��Ŀ����
��2011•˳������ģ����֪��ԲC�����ҽ�������ֱ�ΪF1(-
��0)��F2(
��0)����������
����ԲC�����Ҷ���ֱ��ΪA��B����S����ԲC��λ��x���Ϸ��Ķ��㣬ֱ��AS��BS��ֱ��l��x=-
�ֱ���M��N���㣮
��1������ԲC�ķ��̣�
��2�����߶�MN���ȵ���Сֵ��
��3�����߶�MN�ij�����Сʱ������ԲC�ϵ�T���㣺T��ֱ��AS�ľ������
����ȷ����T�ĸ�����
| 3 |
| 3 |
| ||
| 2 |
| 10 |
| 3 |
��1������ԲC�ķ��̣�
��2�����߶�MN���ȵ���Сֵ��
��3�����߶�MN�ij�����Сʱ������ԲC�ϵ�T���㣺T��ֱ��AS�ľ������
| ||
| 4 |
��������1����Ϊ
=
����c=
������a=2��b=
=1���ɴ��������ԲC�ķ��̣�
��2 ����ԲC�����Ҷ�������ΪA��-2��0����B��2��0������ֱ��AS�ķ���Ϊy=k��x+2�����Ӷ�M(-
��-
k)
��
���ã�1+4k2��x2+16k2x+16k2-4=0���ɴ������ܹ�����߶�MN�ij��ȵ���Сֵ��
��3���ɣ�2��֪�����߶�MN�ij���ȡ��Сֵʱ��k=1����ʱAS�ķ���Ϊx-y+2=0��S(-
��
)����Ϊ��T��ֱ��AS�ľ������
�����Ե�T��ƽ����AS����AS�������
��ֱ��l���ϣ���l�䣺x-y+t=0������
=
�����t=
��t=
���ɴ���������������T�ĸ�����
| c |
| a |
| ||
| 2 |
| 3 |
| a2-c2 |
��2 ����ԲC�����Ҷ�������ΪA��-2��0����B��2��0������ֱ��AS�ķ���Ϊy=k��x+2�����Ӷ�M(-
| 10 |
| 3 |
| 4 |
| 3 |
��
|
��3���ɣ�2��֪�����߶�MN�ij���ȡ��Сֵʱ��k=1����ʱAS�ķ���Ϊx-y+2=0��S(-
| 6 |
| 5 |
| 4 |
| 5 |
| ||
| 4 |
| ||
| 4 |
| |t-2| | ||
|
| ||
| 4 |
| 3 |
| 2 |
| 5 |
| 2 |
����⣺��1����Ϊ
=
����c=
������a=2��b=
=1
������ԲC�ķ���Ϊ
+y2=1������3�֣�
��2 �� ��֪��ԲC�����Ҷ�������ΪA��-2��0����B��2��0����ֱ��AS��б��k��Ȼ���ڣ���k��0
�ʿ���ֱ��AS�ķ���Ϊy=k��x+2�����Ӷ�M(-
��-
k)
��
���ã�1+4k2��x2+16k2x+16k2-4=0
��S��x1��y1������(-2)x1=
����x1=
�Ӷ�y1=
����S(
��
)��B��2��0������ֱ��BS�ķ���Ϊy=-
(x-2)
��
��
������N(-
��
)��|MN|=|
+
|
��k��0������|MN|=
+
��2
=
���ҽ���
=
ʱ����k=1ʱ�Ⱥų���
����k=1ʱ���߶�MN�ij���ȡ��Сֵ
��..��9�֣�
��3���ɣ�2��֪�����߶�MN�ij���ȡ��Сֵʱ��k=1
��ʱAS�ķ���Ϊx-y+2=0��S(-
��
)��
��Ϊ��T��ֱ��AS�ľ������
��
���Ե�T��ƽ����AS����AS�������
��ֱ��l����
��l�䣺x-y+t=0������
=
�����t=
��t=
1��t=
2ʱ����
6��5x2+12x+5=07
���ڡ�=44��0����ֱ��l������ԲC��������ͬ����
��t=
ʱ����
��5x2+20x+21=0���ڡ�=-20��0����ֱ��l������ԲCû�н���
���������T�ĸ�����2����..��14�֣�
| c |
| a |
| ||
| 2 |
| 3 |
| a2-c2 |
������ԲC�ķ���Ϊ
| x2 |
| 4 |
��2 �� ��֪��ԲC�����Ҷ�������ΪA��-2��0����B��2��0����ֱ��AS��б��k��Ȼ���ڣ���k��0
�ʿ���ֱ��AS�ķ���Ϊy=k��x+2�����Ӷ�M(-
| 10 |
| 3 |
| 4 |
| 3 |
��
|
��S��x1��y1������(-2)x1=
| 16k2-4 |
| 1+4k2 |
| 2-8k2 |
| 1+4k2 |
�Ӷ�y1=
| 4k |
| 1+4k2 |
| 2-8k2 |
| 1+4k2 |
| 4k |
| 1+4k2 |
| 1 |
| 4k |
��
|
|
| 10 |
| 3 |
| 4 |
| 3k |
| 4k |
| 3 |
| 4 |
| 3k |
��k��0������|MN|=
| 4k |
| 3 |
| 4 |
| 3k |
|
| 8 |
| 3 |
���ҽ���
| 4k |
| 3 |
| 4 |
| 3k |
����k=1ʱ���߶�MN�ij���ȡ��Сֵ
| 8 |
| 3 |
��3���ɣ�2��֪�����߶�MN�ij���ȡ��Сֵʱ��k=1
��ʱAS�ķ���Ϊx-y+2=0��S(-
| 6 |
| 5 |
| 4 |
| 5 |
��Ϊ��T��ֱ��AS�ľ������
| ||
| 4 |
���Ե�T��ƽ����AS����AS�������
| ||
| 4 |
��l�䣺x-y+t=0������
| |t-2| | ||
|
| ||
| 4 |
| 3 |
| 2 |
| 5 |
| 2 |
1��t=
| 3 |
| 2 |
|
���ڡ�=44��0����ֱ��l������ԲC��������ͬ����
��t=
| 5 |
| 2 |
|
���������T�ĸ�����2����..��14�֣�
������������Ҫ������Բ�����̣��������ʣ�ֱ������Բ��λ�ù�ϵ����������漰���켣���̵���ֱ������Բ�����֪ʶ������ʱҪע������ؽ��еȼ�ת���������������������������֤���������麯���뷽��˼�룬������ת��˼�룮

��ϰ��ϵ�д�
 ��ѧʵ����ϵ�д�
��ѧʵ����ϵ�д�
�����Ŀ
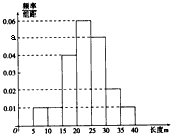 ��2011•˳������ģ��ij�ij�Ϊ�˽�һ����������������������100������ά�ij��ȣ�����ά�ij���������������Ҫָ�꣩���������ݾ�������[5��40]�У���Ƶ�ʷֲ�ֱ��ͼ��ͼ��ʾ����ͼ�����ݿ�֪a=
��2011•˳������ģ��ij�ij�Ϊ�˽�һ����������������������100������ά�ij��ȣ�����ά�ij���������������Ҫָ�꣩���������ݾ�������[5��40]�У���Ƶ�ʷֲ�ֱ��ͼ��ͼ��ʾ����ͼ�����ݿ�֪a=