题目内容
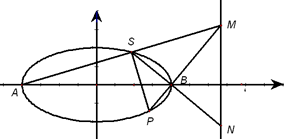
已知椭圆C: 与双曲线
与双曲线 -y2=1有公共焦点,且离心率为
-y2=1有公共焦点,且离心率为 .A,B分别是椭圆C的左顶点和右顶点.点S是椭圆C上位于x轴上方的动点.直线AS,BS分别与直线l:x=
.A,B分别是椭圆C的左顶点和右顶点.点S是椭圆C上位于x轴上方的动点.直线AS,BS分别与直线l:x= 分别交于M,N两点.
分别交于M,N两点.(1)求椭圆C的方程;
(2)延长MB交椭圆C于点P,若PS⊥AM,试证明MS2=MB•MP.
(3)当线段MN的长度最小时,在椭圆C上是否存在点T,使得△TSB的面积为
 ?若存在确定点T的个数,若不存在,说明理由.
?若存在确定点T的个数,若不存在,说明理由.
【答案】分析:(1)根据椭圆与双曲线有公共焦点,可确定椭圆的焦点,利用椭圆的离心率,即可求出椭圆的方程;
(2)引入直线AS的斜率k,用点斜式写出直线AS的方程,与l的方程联立求出点M的坐标,与椭圆方程联立,求得点S的坐标,又点B的坐标已知,从而可得 ,利用PS⊥AM,由射影定理可得MS2=MB•MP.
,利用PS⊥AM,由射影定理可得MS2=MB•MP.
(3)线段MN的长度可以表示成直线AS的斜率k的函数,根据其形式利用基本不等式法求最值,从而求出直线SB的方程要使椭圆C上存在点T,使得△TSB的面积等于 ,只须T到直线BS的距离等于
,只须T到直线BS的距离等于 ,由此问题转化为研究与直线SB平行且距离为
,由此问题转化为研究与直线SB平行且距离为 的直线与椭圆的交点个数问题.
的直线与椭圆的交点个数问题.
解答:(1)解:∵椭圆C: 与双曲线
与双曲线 -y2=1有公共焦点
-y2=1有公共焦点
∴椭圆C的焦点为 ,
,
∴ ,
,
又∵ ,
,
∴a=2,b=1,
∴椭圆的方程为 .…(3分)
.…(3分)
(2)证明:直线AS的斜率k显然存在,且k>0,故可设直线AS的方程为y=k(x+2),从而
由 得(1+4k2)x2+16k2x+16k2-4=0
得(1+4k2)x2+16k2x+16k2-4=0
设S(x1,y1),则 得
得 ,从而
,从而 …(5分)
…(5分)
即
又B(2,0),从而 ,
,
∴ ,
,
∴ ,
,
又因为PS⊥AM,由射影定理可得MS2=MB•MP.…(7分)
(3)解:由 得
得
∴
又k>0,∴
当且仅当 ,即
,即 时等号成立
时等号成立
∴ 时,线段MN的长度取最小值
时,线段MN的长度取最小值
此时BS的方程为 ,∴
,∴ …(9分)
…(9分)
要使椭圆C上存在点T,使得△TSB的面积等于 ,只须T到直线BS的距离等于
,只须T到直线BS的距离等于 ,
,
所以T在平行于BS且与BS距离等于 的直线l'上.
的直线l'上.
设直线l':x+y+t=0,则由 ,解得
,解得 或
或 .
.
当 时,由
时,由 ,得5x2-12x+5=0
,得5x2-12x+5=0
由于△=44>0,故直线l'与椭圆C有两个不同的交点;
当 时,由
时,由 得5x2-20x+21=0,
得5x2-20x+21=0,
由于△=-20<0,故直线l'与椭圆没有交点.
综上所述,当线段MN的长度最小时,在椭圆C上仅存在两个不同的点T,使得△TSB的面积为 .…(12分)
.…(12分)
点评:本题的考点是直线与圆锥曲线的综合问题,要求答题者拥有较高的探究转化能力以及对直线与圆锥曲线位置关系中特征有较好的理解,正确理解题意,合理转化是解题的关键.
(2)引入直线AS的斜率k,用点斜式写出直线AS的方程,与l的方程联立求出点M的坐标,与椭圆方程联立,求得点S的坐标,又点B的坐标已知,从而可得
 ,利用PS⊥AM,由射影定理可得MS2=MB•MP.
,利用PS⊥AM,由射影定理可得MS2=MB•MP.(3)线段MN的长度可以表示成直线AS的斜率k的函数,根据其形式利用基本不等式法求最值,从而求出直线SB的方程要使椭圆C上存在点T,使得△TSB的面积等于
 ,只须T到直线BS的距离等于
,只须T到直线BS的距离等于 ,由此问题转化为研究与直线SB平行且距离为
,由此问题转化为研究与直线SB平行且距离为 的直线与椭圆的交点个数问题.
的直线与椭圆的交点个数问题.解答:(1)解:∵椭圆C:
 与双曲线
与双曲线 -y2=1有公共焦点
-y2=1有公共焦点∴椭圆C的焦点为
 ,
,∴
 ,
,又∵
 ,
,∴a=2,b=1,
∴椭圆的方程为
 .…(3分)
.…(3分)(2)证明:直线AS的斜率k显然存在,且k>0,故可设直线AS的方程为y=k(x+2),从而

由
 得(1+4k2)x2+16k2x+16k2-4=0
得(1+4k2)x2+16k2x+16k2-4=0设S(x1,y1),则
 得
得 ,从而
,从而 …(5分)
…(5分)即

又B(2,0),从而
 ,
,
∴
 ,
,∴
 ,
,又因为PS⊥AM,由射影定理可得MS2=MB•MP.…(7分)
(3)解:由
 得
得
∴

又k>0,∴

当且仅当
 ,即
,即 时等号成立
时等号成立∴
 时,线段MN的长度取最小值
时,线段MN的长度取最小值
此时BS的方程为
 ,∴
,∴ …(9分)
…(9分)要使椭圆C上存在点T,使得△TSB的面积等于
 ,只须T到直线BS的距离等于
,只须T到直线BS的距离等于 ,
,所以T在平行于BS且与BS距离等于
 的直线l'上.
的直线l'上.设直线l':x+y+t=0,则由
 ,解得
,解得 或
或 .
.当
 时,由
时,由 ,得5x2-12x+5=0
,得5x2-12x+5=0由于△=44>0,故直线l'与椭圆C有两个不同的交点;
当
 时,由
时,由 得5x2-20x+21=0,
得5x2-20x+21=0,由于△=-20<0,故直线l'与椭圆没有交点.
综上所述,当线段MN的长度最小时,在椭圆C上仅存在两个不同的点T,使得△TSB的面积为
 .…(12分)
.…(12分)点评:本题的考点是直线与圆锥曲线的综合问题,要求答题者拥有较高的探究转化能力以及对直线与圆锥曲线位置关系中特征有较好的理解,正确理解题意,合理转化是解题的关键.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
 与双曲线C2:
与双曲线C2: 有公共的焦点,C2的一条渐近线与以C1的长轴为直径的圆相交于A、B两点,C1恰好将线段AB三等分,则( )
有公共的焦点,C2的一条渐近线与以C1的长轴为直径的圆相交于A、B两点,C1恰好将线段AB三等分,则( ) B.
B. C.
C. D.
D.
 已知椭圆C:
已知椭圆C: 与双曲线
与双曲线 -y2=1有公共焦点,且离心率为
-y2=1有公共焦点,且离心率为 .A,B分别是椭圆C的左顶点和右顶点.点S是椭圆C上位于x轴上方的动点.直线AS,BS分别与直线l:x=
.A,B分别是椭圆C的左顶点和右顶点.点S是椭圆C上位于x轴上方的动点.直线AS,BS分别与直线l:x= 分别交于M,N两点.
分别交于M,N两点. ?若存在确定点T的个数,若不存在,说明理由.
?若存在确定点T的个数,若不存在,说明理由. 与双曲线
与双曲线 -y2=1有公共焦点,且离心率为
-y2=1有公共焦点,且离心率为 .A,B分别是椭圆C的左顶点和右顶点.点S是椭圆C上位于x轴上方的动点.直线AS,BS分别与直线l:x=
.A,B分别是椭圆C的左顶点和右顶点.点S是椭圆C上位于x轴上方的动点.直线AS,BS分别与直线l:x= 分别交于M,N两点.
分别交于M,N两点. ?若存在确定点T的个数,若不存在,说明理由.
?若存在确定点T的个数,若不存在,说明理由.