题目内容
(本题满分10分)
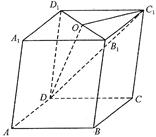
如图,ABCD是边长为2的正方形,O是正方形的中心,PO 底面ABCD,PO=
底面ABCD,PO= ,E是PC的中点。
,E是PC的中点。

求证:(1)PA∥平面BDE;(2)直线PA与平面PBD所成的角.
如图,ABCD是边长为2的正方形,O是正方形的中心,PO
 底面ABCD,PO=
底面ABCD,PO= ,E是PC的中点。
,E是PC的中点。
求证:(1)PA∥平面BDE;(2)直线PA与平面PBD所成的角.
解: 证明(Ⅰ)∵O是AC的中点,E是PC的中点,∴OE∥AP,又∵OE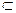 平面BDE,PA
平面BDE,PA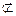 平面BDE,∴PA∥平面BDE.
平面BDE,∴PA∥平面BDE.
(Ⅱ)连接AC∵PO 底面ABCD,∴PO
底面ABCD,∴PO AC,又∵AC
AC,又∵AC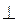 BD,且BD
BD,且BD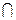 PO=O
PO=O
∴AC 平面PBD,∴∠APO即为所求角,
平面PBD,∴∠APO即为所求角,
∵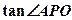 =AO/PO=
=AO/PO=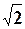 /
/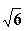 =
= /3;∴
/3;∴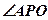 =300
=300
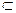 平面BDE,PA
平面BDE,PA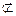 平面BDE,∴PA∥平面BDE.
平面BDE,∴PA∥平面BDE.(Ⅱ)连接AC∵PO
 底面ABCD,∴PO
底面ABCD,∴PO AC,又∵AC
AC,又∵AC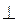 BD,且BD
BD,且BD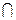 PO=O
PO=O∴AC
 平面PBD,∴∠APO即为所求角,
平面PBD,∴∠APO即为所求角, ∵
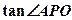 =AO/PO=
=AO/PO=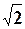 /
/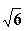 =
= /3;∴
/3;∴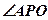 =300
=300略

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 ,直线
,直线 平面
平面 ,有下列四个命题:①
,有下列四个命题:① ,②
,② l∥m,③l∥m
l∥m,③l∥m ,④
,④
 ∥
∥
 ∥平面
∥平面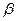 ,
,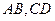 是夹在
是夹在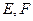 分
分 别是
别是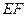 与
与
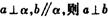

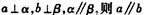
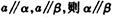
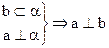 ;②
;②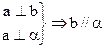 ;③
;③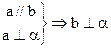 ;④
;④
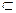 α,b
α,b