题目内容
12.已知函数f(x)=lg(ax-bx)(a>1>b>0).(1)求y=f(x)的定义域;
(2)若f(2x2-mx)>f(x-1)在(1,3)恒成立,求m的取值范围;
(3)当a=4b时,g(x)=f(x)-lg(ax+bx)-n在(1,2)上有零点,求n的取值范围.
分析 (1)利用对数函数和指数函数的定义域及单调性即可得出;
(2)先判断函数f(x)的单调性,根据单调性得到2x2-mx>x-1在(1,3)恒成立,分离参数,构造函数,求出函数的最值,问题得以解决,
(3)化简g(x),根据零点存在定理即可求出n的取值范围.
解答 解:(1)要使函数有意义,必有ax-bx>0,a>1>b>0
可得($\frac{a}{b}$)x>1,解得x>0,
函数的定义域为:(0,+∞);
(2)设φ(x)=ax-bx,再设x1,x2∈(0,+∞)上的任意两个数,且x1<x2,
则φ(x1)-φ(x2)=${a}^{{x}_{1}}-{b}^{{x}_{1}}-{a}^{{x}_{2}}+{b}^{{x}_{2}}$=(${a}^{{x}_{1}}-{a}^{{x}_{2}}$)+(${b}^{{x}_{2}}-{b}^{{x}_{1}}$),
对于函数y=ax为增函数,y=bx为减函数,
∴${a}^{{x}_{1}}-{a}^{{x}_{2}}$<0,${b}^{{x}_{2}}-{b}^{{x}_{1}}$<0,
∴φ(x1)-φ(x2)<0,
∴φ(x)在(0,+∞)为增函数,
∵y=lgx在(0,+∞)为增函数,
∴f(x)在(0,+∞)为增函数;
∵f(2x2-mx)>f(x-1)在(1,3)恒成立
∴2x2-mx>x-1在(1,3)恒成立,
∴m<2x+$\frac{1}{x}$-1,
设h(x)=2x+$\frac{1}{x}$-1,
则h′(x)=2-$\frac{1}{{x}^{2}}$>0,
∴h(x)=2x+$\frac{1}{x}$-1在(1,3)上单调递增,
∴h(x)>h(1)=2+1-1=2,
∴m≤2,
∴m的取值范围为(-∞,2];
(3)当a=4b时,g(x)=f(x)-lg(ax+bx)-n=lg(ax-bx)-lg(ax+bx)-n=lg($\frac{{4}^{x}-1}{{4}^{x}+1}$)-n,
∵g(x)在(1,2)上有零点,
∴g(1)g(2)<0,
∴(lg$\frac{3}{5}$-n)(lg$\frac{15}{17}$-n)<0,
即(n-lg$\frac{3}{5}$)(n-lg$\frac{15}{17}$-n)<0,
解得lg$\frac{3}{5}$<n<lg$\frac{15}{17}$,
∴n的取值范围(lg$\frac{3}{5}$,lg$\frac{15}{17}$).
点评 本题主要考查了对数函数的定义域,以及函数的单调性的判定和应用,以及函数恒成立问题和函数的零点存在定理,同时考查了计算能力,属于中档题.

 名校课堂系列答案
名校课堂系列答案| A. | c>a>b | B. | a>b>c | C. | c>b>a | D. | c>b>a |
| A. | 正方体、球、侧棱两两垂直且相等的正三棱锥 | |
| B. | 正方体、球、各棱长都相等的正三棱柱 | |
| C. | 球、高和底面半径相等的圆柱、高和底面半径相等的圆锥 | |
| D. | 正方体、正四棱台、棱长相等的平行六面体 |
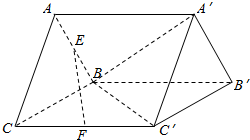 已知三棱柱ABC-A′B′C′如图所示,四边形BCC′B′为菱形,∠BCC′=60°,△ABC为等边三角形,面ABC⊥面BCC′B′,E、F分别为棱AB、CC′的中点.
已知三棱柱ABC-A′B′C′如图所示,四边形BCC′B′为菱形,∠BCC′=60°,△ABC为等边三角形,面ABC⊥面BCC′B′,E、F分别为棱AB、CC′的中点.