Question

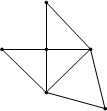
已知腰长为a的等腰△ABC中，∠ACB=90°，当A、B分别在x轴、y轴的正半轴上移动时（C与原点在AB的两侧），求OC的最大值．

Answer 1

解：如图，由于∠AOB=∠ACB=90°，
∴O、B、C、A四点共圆．其直径是AB=．
当OC为此圆直径为最大，
∴（OC）_max=AB=．
则OC的最大值：．
分析：根据题意画出图形，如图，由于∠AOB=∠ACB=90°，得出四点共圆．然后利用圆的性质求得OC的最大值即可．
点评：本题主要考查点、线、面间的距离计算．解题的关键是根据题意确定O、B、C、A四点共圆，借助平面几何的性质解决问题．