题目内容
在 中,
中, 的对边分别为
的对边分别为 ,且
,且 .
.
(1)求 的值;
的值;
(2)若 ,
, ,求
,求 和
和 .
.
(1) ;(2)
;(2) .
.
解析试题分析:(1)由正弦定理得 ,
, ,
,
又 ,∴
,∴ ,… 2分
,… 2分
即 ,∴
,∴ ,… 4分
,… 4分
∴ ,又
,又 ,∴
,∴ 6分
6分
(2)由 得
得 ,又
,又 ,∴
,∴ 8分
8分
由 ,
, 可得
可得 , 10分
, 10分
∴ ,即
,即 ,∴
,∴ . 12分
. 12分
考点:本题主要考查平面向量的数量积,两角和与差的三角函数,正弦定理、余弦定理的应用。
点评:典型题,近些年来,将平面向量、三角函数、三角形问题等结合考查,已成较固定模式。研究三角函数问题时,往往要利用三角公式先行“化一”。本题(2)通过构建a,c的方程组,求得a,c。

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案
相关题目
 是角
是角 所对的边,且
所对的边,且 .
. 的大小;(2)若
的大小;(2)若 ,求△ABC周长的最大值。
,求△ABC周长的最大值。 +cos A=0.
+cos A=0. ,b+c=4,求△ABC的面积.
,b+c=4,求△ABC的面积.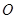 为圆心、
为圆心、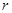 公里为半径的圆形保护区,从保护区边缘起,在城中心
公里为半径的圆形保护区,从保护区边缘起,在城中心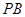 、西南方向上有一条一级公路
、西南方向上有一条一级公路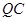 ,现要在保护区边缘PQ弧上选择一点A作为出口,建一条连接两条公路且与圆
,现要在保护区边缘PQ弧上选择一点A作为出口,建一条连接两条公路且与圆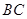 .已知通往一级公路的道路
.已知通往一级公路的道路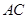 每公里造价为
每公里造价为 万元,通往高速公路的道路
万元,通往高速公路的道路 每公里造价是
每公里造价是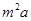 万元,其中
万元,其中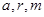 为常数,设
为常数,设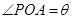 ,总造价为
,总造价为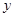 万元.
万元.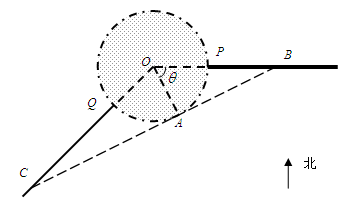
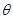 的函数
的函数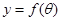 ,并求出定义域;
,并求出定义域;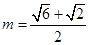 时,如何确定A点的位置才能使得总造价最低?
时,如何确定A点的位置才能使得总造价最低? =
= .
. ,b=2
,b=2 ,求a和c的值.
,求a和c的值. ,向量
,向量
 ,且满足
,且满足 。
。 ,求角
,求角 ;
; ,△ABC的面积
,△ABC的面积 ,求△ABC的周长。
,求△ABC的周长。
 ;
;
 ,解三角形ABC。
,解三角形ABC。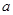 、
、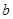 、
、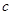 分别是
分别是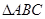 的三个内角
的三个内角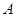 、
、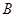 、
、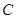 所对的边
所对的边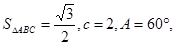 求
求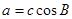 ,且
,且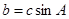 ,试判断
,试判断