题目内容
6.设实数x,y满足约束条件$\left\{\begin{array}{l}x-y≥-1\\ x+y≤4\\ y≥a\end{array}\right.$,目标函数z=3x-2y的最小值为-4,则z的最大值为17.分析 作出可行域,变形目标函数并平移直线y=$\frac{3}{2}$x,作出最优解,代入方程求解a可得结论,然后求z的最大值.
解答 解:作出约束条件所对应的可行域(如图),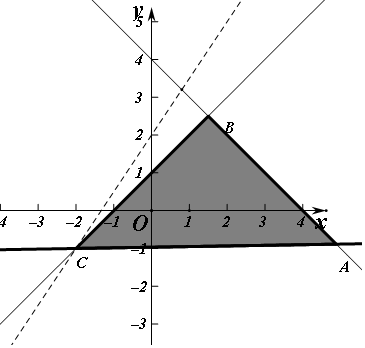
目标函数z=3x-2y可化为y=$\frac{3}{2}$x-$\frac{z}{2}$z,平移直线y=$\frac{3}{2}$x可知,
当直线经过点C(-2,-1)时,
截距取最大值,z最小,
∴(-2,-1)在直线y=a上所以a=2,
所以直线z=3x-2y经过图中A(5,-1)时在y轴截距最小,z最大为3×5-(-2)=17;
故答案为:17.
点评 本题考查简单线性规划,准确作图、利用目标函数的几何意义求最值是解决问题的关键,属中档题

练习册系列答案
相关题目
17.交强险是车主必须为机动车购买的险种,若普通6座以下私家车投保交强险第一年的费用(基准保费)统一为a元,在下一年续保时,实行的是费率浮动机制,保费与上一年度车辆发生道路交通事故的情况相联系,发生交通事故的次数越多,费率也就越高,具体浮动情况如表:
某机构为了研究某一品牌普通6座以下私家车的投保情况,随机抽取了60辆车龄已满三年的该品牌同型号私家车的下一年续保时的情况,统计得到了下面的表格:
以这60辆该品牌车的投保类型的频率代替一辆车投保类型的概率,完成下列问题:
(1)求一辆普通6座以下私家车在第四年续保时保费高于基本保费的概率;
(2)某二手车销售商专门销售这一品牌的二手车,且将下一年的交强险保费高于基本保费的车辆记为事故车,假设购进一辆事故车亏损5000元,一辆非事故车盈利10000元,且各种投保类型车的频率与上述机构调查的频率一致,完成下列问题:
①若该销售商店内有6辆(车龄已满三年)该品牌二手车,某顾客欲在店内随机挑选两辆车,求这两车辆中恰好有一辆事故车的概率;
②若该销售商一次购进120辆(车龄已满三年)该品牌的二手车,求一辆车盈利的平均值.
| 交强险浮动因素和浮动费率比率表 | ||
| 浮动因素 | 浮动比率 | |
| A1 | 上一个年度未发生有责任道路交通事故 | 下浮10% |
| A2 | 上两个年度未发生有责任道路交通事故 | 下浮20% |
| A3 | 上三个及以上年度未发生有责任道路交通事故 | 下浮30% |
| A4 | 上一个年度发生一次有责任不涉及死亡的道路交通事故 | 0% |
| A5 | 上一个年度发生两次及两次以上有责任道路交通事故 | 上浮10% |
| A6 | 上一个年度发生有责任道路交通死亡事故 | 上浮30% |
| 类型 | A1 | A2 | A3 | A4 | A5 | A6 |
| 数量 | 10 | 5 | 5 | 20 | 15 | 5 |
(1)求一辆普通6座以下私家车在第四年续保时保费高于基本保费的概率;
(2)某二手车销售商专门销售这一品牌的二手车,且将下一年的交强险保费高于基本保费的车辆记为事故车,假设购进一辆事故车亏损5000元,一辆非事故车盈利10000元,且各种投保类型车的频率与上述机构调查的频率一致,完成下列问题:
①若该销售商店内有6辆(车龄已满三年)该品牌二手车,某顾客欲在店内随机挑选两辆车,求这两车辆中恰好有一辆事故车的概率;
②若该销售商一次购进120辆(车龄已满三年)该品牌的二手车,求一辆车盈利的平均值.
11.已知函数$f(x)=sin({ωx-\frac{π}{6}})+\frac{1}{2}({ω>0})$,且$f(α)=-\frac{1}{2}$,$f(β)=\frac{1}{2}$,若|α-β|的最小值为$\frac{3π}{4}$,则ω的值为( )
| A. | 1 | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | 2 |
18.已知等差数列{an}的公差d>0,且a2,a5-1,a10成等比数列,若a1=5,Sn为数列{an}的前n项和,则$\frac{{2{S_n}+n+32}}{{{a_n}+1}}$的最小值为( )
| A. | $3\sqrt{3}$ | B. | $2\sqrt{7}$ | C. | $\frac{20}{3}$ | D. | $\frac{17}{3}$ |
15. 如图,已知三棱锥A-BPC中,AP⊥PC,AC⊥BC,M为AB的中点,D为PB的中点,且△PMB为正三角形.
如图,已知三棱锥A-BPC中,AP⊥PC,AC⊥BC,M为AB的中点,D为PB的中点,且△PMB为正三角形.
(1)求证:BC⊥平面APC;
(2)若BC=6,AB=20,求三棱锥D-BCM的体积.
 如图,已知三棱锥A-BPC中,AP⊥PC,AC⊥BC,M为AB的中点,D为PB的中点,且△PMB为正三角形.
如图,已知三棱锥A-BPC中,AP⊥PC,AC⊥BC,M为AB的中点,D为PB的中点,且△PMB为正三角形.(1)求证:BC⊥平面APC;
(2)若BC=6,AB=20,求三棱锥D-BCM的体积.
10.设点P是圆C:(x+4)2+(y-2)2=5上的动点,则点P到原点距离的最大值为( )
| A. | $\sqrt{5}$ | B. | $2\sqrt{5}$ | C. | $3\sqrt{5}$ | D. | $4\sqrt{5}$ |
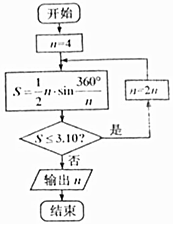 公元263年左右,我国数学家刘徽发现当圆内接正多边形的边数无限增加时,多边形面积可无限逼近圆的面积,并创立了“割圆术”.利用“割圆术”刘徽得到了圆周率精确到小数点后两位的近似值3.14,这就是著名的“徽率”.如图是利用刘徽的“割圆术”思想设计的一个程序框图,则输出n的值为( )(参考数据:sin22.5°=0.3827,sin11.25°=0.1951,sin5.625°=0.0980)
公元263年左右,我国数学家刘徽发现当圆内接正多边形的边数无限增加时,多边形面积可无限逼近圆的面积,并创立了“割圆术”.利用“割圆术”刘徽得到了圆周率精确到小数点后两位的近似值3.14,这就是著名的“徽率”.如图是利用刘徽的“割圆术”思想设计的一个程序框图,则输出n的值为( )(参考数据:sin22.5°=0.3827,sin11.25°=0.1951,sin5.625°=0.0980)