题目内容

12．设集合A={x|（x+4）（x+1）=0}，集合B={x|（x-4）（x-1）=0}，则A∩B=（　　）
A．{-1，-4}B．{0}C．{1，4}D．∅

分析 解方程求出集合A、B，根据交集的定义写出A∩B．

解答 解：集合A={x|（x+4）（x+1）=0}={x|x=-4或x=-1}={-4，-1}，
集合B={x|（x-4）（x-1）=0}={x|x=4或x=1}={1，4}，
则A∩B=∅．
故选：D．

点评 本题考查了解方程和集合的基本运算问题，是基础题．

练习册系列答案
相关题目
2．已知角α的终边经过点（3a-9，a+2），且sin2α≤0，sinα＞0，则a的取值范围是（　　）
A．（-2，3）B．[-2，3）C．（-2，3]D．[-2，3]
3．已知椭圆$C：\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（a＞b＞0）$的离心率为$\frac{{\sqrt{2}}}{2}$，F为C的右焦点，E为C的上顶点，坐标原点O到直线EF的距离为$\sqrt{2}$．
（1）求椭圆C的方程；
（2）过点$（0，-\frac{2}{3}）$且斜率为k的直线l与椭圆C交于A，B两点，在y轴上是否存在定点M，使以AB为直径的圆恒过点M？若存在，求出点M的坐标；若不存在，说明理由．
20．已知命题p：方程$\frac{{x}^{2}}{m+1}$+$\frac{{y}^{2}}{3-m}$=1表示焦点在y轴上的椭圆，命题q：关于x的方程x2+2mx+m+3=0无实根．
（1）若命题p为真命题，求实数m的取值范围；
（2）若“p∧q”为假命题，“p∨q”为真命题，求实数m的取值范围．
7．已知四棱锥P-ABCD中，平面PCD⊥平面ABCD，且PD=PC=$\frac{\sqrt{2}}{2}$CD=$\frac{\sqrt{2}}{2}$BC，∠BCD=$\frac{2π}{3}$，△ABD是等边三角形，AC∩BD=E．
（1）证明：PC⊥平面PAD；
（2）求二面角P-AB-C的余弦值．
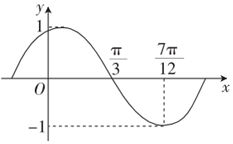17．已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，-$\frac{π}{2}$＜φ＜$\frac{π}{2}$），其部分图象如图所示．
（1）求函数 y=f（x）的解析式；
（2）若α∈（0，$\frac{π}{2}$），且cos（$\frac{π}{2}$+α）=-$\frac{3}{5}$，求f（α）的值．
4．设点A、F（c，0）分别是双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1（a＞0，b＞0）$的右顶点、右焦点，直线$x=\frac{a^2}{c}$交该双曲线的一条渐近线于点P．若△PAF是等腰三角形，则此双曲线的离心率为2．
1．已知函数f（x）=$\frac{\sqrt{3}}{2}$sin2x-cos2x+$\frac{1}{2}$
（Ⅰ）求函数f（x）=0时x的集合；
（Ⅱ）求函数f（x）在区间[0，$\frac{π}{2}$]上的最小值．
2．已知函数$f（x）=cosx-cos（x+\frac{π}{2}），x∈R$
（1）求f（x）的最小正周期；
（2）求f（x）的最大值和最小值，以及取得最大值和最小值时x的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网