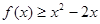题目内容
已知二次函数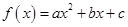 .
.
(1)若对任意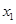 、
、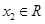 ,且
,且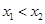 ,都有
,都有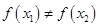 ,求证:关于
,求证:关于 的方程
的方程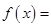
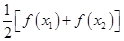 有两个不相等的实数根且必有一个根属于
有两个不相等的实数根且必有一个根属于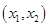 ;
;
(2)若关于 的方程
的方程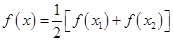 在
在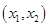 上的根为
上的根为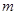 ,且
,且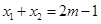 ,设函数
,设函数 的图象的对称轴方程为
的图象的对称轴方程为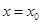 ,求证:
,求证: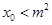 .
.
(1)详见解析;(2)详见解析.
解析试题分析:(1)先构造新函数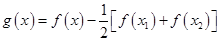 ,利用
,利用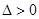 证明方程
证明方程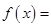
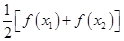 有两个不相等的实数根,然后利用存在定理证明方程
有两个不相等的实数根,然后利用存在定理证明方程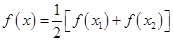 必有一个根属于
必有一个根属于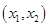 ,即利用
,即利用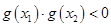 来证明;(2)将
来证明;(2)将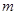 的代入方程
的代入方程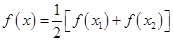 得到
得到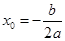 的表达式,结合
的表达式,结合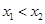 证明
证明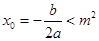 .
.
试题解析:(1)构造函数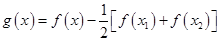

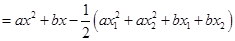 ,
,
由于函数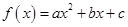 为二次函数,所以
为二次函数,所以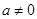 ,
,
对于二次函数 而言,
而言,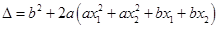
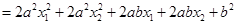
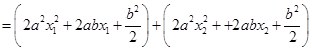
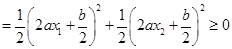 ,
,
若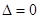 ,则有
,则有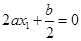 且有
且有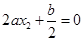 ,从而有
,从而有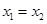 ,这与
,这与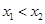 矛盾,
矛盾,
故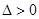 ,故方程
,故方程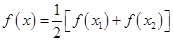 有两个不相等,
有两个不相等,
由于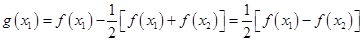 ,
,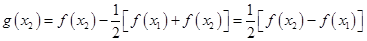 ,
,
所以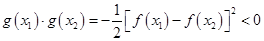 ,
,
由零点存在定理知,方程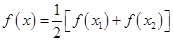 必有一个根属于
必有一个根属于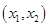 ;
;
(2)由题意知 ,化简得
,化简得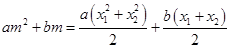 ,
,
即 ,则有
,则有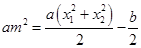 ,
,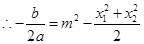 ,
,
由于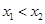 ,则
,则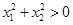 ,故
,故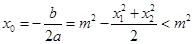 ,即
,即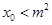 .
.
考点:1.二次方程根的个数的判断;2.零点存在定理;3.二次函数图象的对称轴

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
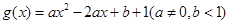 在区间
在区间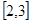 上有最大值4,最小值1,
上有最大值4,最小值1, 的值。
的值。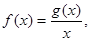 不等式
不等式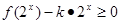 在区间
在区间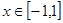 上恒成立,求实数k的取值范围?
上恒成立,求实数k的取值范围? (
( 为常数,
为常数, 为自然对数的底)
为自然对数的底)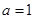 时,求
时,求 的单调区间;
的单调区间; 上无零点,求
上无零点,求 ,在
,在 上存在两个不同的
上存在两个不同的 使得
使得 成立,求
成立,求 的表达式;
的表达式; 的函数
的函数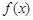 满足
满足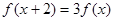 ,当
,当 ∈
∈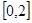 时,
时,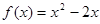
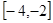 时,求
时,求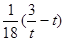 恒成立,求实数
恒成立,求实数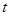 的取值范围.
的取值范围.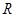 上的函数
上的函数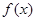 对任意
对任意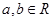 都有
都有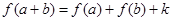 (
(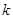 为常数).
为常数).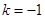 ,
,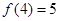 ,若不等式
,若不等式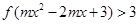 对任意
对任意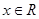 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.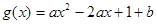 (
(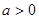 )在区间
)在区间 上有最大值
上有最大值 和最小值
和最小值 .设
.设 ,
,  、
、 的值;
的值; 在
在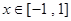 上有解,求实数
上有解,求实数 的取值范围.
的取值范围.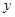 万元与投入
万元与投入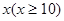 万元之间满足:
万元之间满足: 为常数。当
为常数。当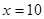 万元时,
万元时,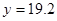 万元;
万元;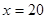 万元时,
万元时,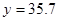 万元。 (参考数据:
万元。 (参考数据: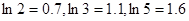 )
) 的解析式;
的解析式; 的最大值。(利润=旅游增加值-投入)。
的最大值。(利润=旅游增加值-投入)。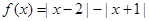 .
.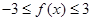 ;
;