题目内容
已知函数f（x）=tanx+cotx+2，且f（2）=m，则f（-2）=
4-m
4-m
．分析：令g（x）=tanx+cotx，则函数g（x）为奇函数，且f（x）=g（x）+2．由f（2）=g（2）+2=m，求得g（2）=m-2，再根据f（-2）=g（-2）+2=-g（2）+2，运算求得结果．
解答：解：令g（x）=tanx+cotx，则函数g（x）为奇函数，且f（x）=g（x）+2．
由于f（2）=g（2）+2=m，∴g（2）=m-2，
∴f（-2）=g（-2）+2=-g（2）+2=2-m+2=4-m，
故答案为 4-m．
由于f（2）=g（2）+2=m，∴g（2）=m-2，
∴f（-2）=g（-2）+2=-g（2）+2=2-m+2=4-m，
故答案为 4-m．
点评：本题主要考查利用函数的奇偶性求函数的值，正切函数的奇偶性，属于中档题．
练习册系列答案
相关题目
-1）+lnx，t为常数，且t＞0．
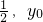）处的切线方程为2x+y-2+ln2，求t和y0的值；
-1）+lnx，t为常数，且t＞0．
）处的切线方程为2x+y-2+ln2，求t和y的值；