题目内容
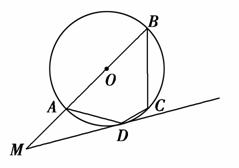
如图，圆O的直径AB＝8，C为圆周上一点，BC＝4，过C作圆的切线l，过A作直线l的垂线AD，D为垂足，AD与圆O交于点E，求线段AE的长．
连接OC、BE、AC，则BE⊥AE.
∵BC＝4，∴OB＝OC＝BC＝4，即△OBC为正三角形，
∴∠CBO＝∠COB＝60°，
又直线l切⊙O于C，
∴∠DCA＝∠CBO＝60°，
∵AD⊥l，∴∠DAC＝90°－60°＝30°，
而∠OAC＝∠ACO＝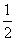
∠COB＝30°，∴∠EAB＝60°，
在Rt△BAE中，∠EBA＝30°，∴AE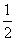＝AB＝4.
练习册系列答案
相关题目
≥2，x＋
＝
＋
＝
＋
≥n＋1(n∈N*)，则a＝________.
D.
，AB是圆O的直径，C为圆O上一点，且BC＝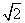
，过点B的圆O的切线交AC延长线于点D，则DA＝________.
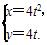(t为参数)上，则|PF|＝( )
(t为参数)与直线l2：
(s为参数)垂直，则k＝______.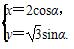
(α为参数)，在极坐标系(与直角坐标系xOy取相同的长度单位，且以原点O为极点，以x轴正半轴为极轴)中，曲线C2的方程为ρ(cosθ－sinθ)＋1＝0，则C1与C2的交点个数为________．
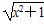图像上的点，Bn(n，bn)为函数y＝x图像上的点，其中n∈N＋，设cn＝an－bn，则cn与cn＋1的大小关系为________．