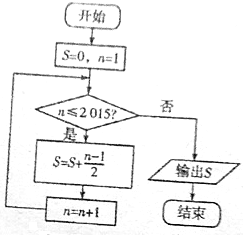
题目内容
18.函数y=lnx-2x在点(1,2)处的切线方程为x+y-3=0.分析 求出函数的导数,求出切线的斜率.
解答 解:函数y=lnx-2x的导数为:y′=$\frac{1}{x}-2$,函数y=lnx-2x在点(1,2)处的切线的斜率为:$y′{|}_{x=1}^{\;}$=-1.所以切线方程为y-2=-(x-1),化简为x+y-3=0.
故答案为:x+y-3=0.
点评 本题考查函数的导数的应用,切线方程的求法,考查计算能力.

练习册系列答案
相关题目
9.设全集为R,集合A={x||x|<3},B={x|-1<x≤5},则A∩(∁RB)=( )
| A. | (-3,0) | B. | (-3,-1] | C. | (-3,-1) | D. | (-3,3) |
7.某商品在5家商场的售价x(元)和销售量y(件)之间的一组数据如下表所示:
由散点图可知,销售量y与价格x之间有较好的线性相关关系,且回归直线方程是$\stackrel{∧}{y}$=-3.2x+4a,则a=10.
| 价格x(元) | 9 | 9.5 | 10 | 10.5 | 11 |
| 销售量y(件) | 11 | a | 8 | 6 | 5 |