题目内容
7.在等差数列{an}中,a1+a2=1,a2016+a2017=3,Sn是数列{an}的前n项和,则S2017=( )| A. | 6051 | B. | 4034 | C. | 2017 | D. | 1009 |
分析 根据题意和等差数列的性质求出a1+a2017的值,由等差数列的前n项和公式求出S2017的值.
解答 解:在等差数列{an}中,
因为a1+a2=1,a2016+a2017=3,
所以a1+a2017=a2+a2016=2,
所以S2017=$\frac{2017({a}_{1}+{a}_{2017})}{2}$=2017,
故选C.
点评 本题考查等差数列的性质、前n项和公式的灵活应用,属于基础题.

练习册系列答案
 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
17.在数列{an}中,已知a1=3,且数列{an+(-1)n}是公比为2的等比数列,对于任意的n∈N*,不等式a1+a2+…+an≥λan+1恒成立,则实数λ的取值范围是( )
| A. | $({-∞,\frac{2}{5}}]$ | B. | $({-∞,\frac{1}{2}}]$ | C. | $({-∞,\frac{2}{3}}]$ | D. | (-∞,1] |
18.执行如图所示的程序框图,若输入a,b,c分别为1,2,0.3,则输出的结果为( )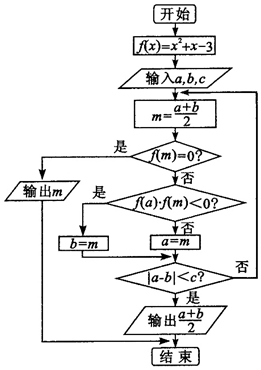

| A. | 1.125 | B. | 1.25 | C. | 1.3125 | D. | 1.375 |
15.我国古代数学名著《九章算术》有“米谷粒分”题:粮仓开仓收粮,有人送来米1536石,验得米内夹谷,抽样取米一把,数得224粒内夹谷28粒,则这批米内夹谷约为( )
| A. | 169石 | B. | 192石 | C. | 1367石 | D. | 1164石 |
12.已知定义在(0,+∞)上的函数f(x)满足f(xy)+$\frac{1}{2}$-f(x)-f(y)=0,若一族平行线x=xi(i=1,2,…,n)分别与y=f(x)图象的交点为(x1,y1),(x2,y2),…,(xn,yn),且xi,2f(1),xn-i+1成等比数列,其中i=1,2,…,n,则$\frac{\sum_{i=1}^{n}{y}_{i}}{n}$=( )
| A. | 2n | B. | 1 | C. | $\frac{1}{2}$ | D. | $\frac{n}{2}$ |
19.现有1000根某品种的棉花纤维,从中随机抽取50根,纤维长度(单位:mm)的数据分组及各组的频数如表,据此估计这1000根中纤维长度不小于37.5mm的根数是180.
| 纤维长度 | 频数 |
| [22.5,25.5) | 3 |
| [25.5,28.5) | 8 |
| [28.5,31.5) | 9 |
| [31.5,34.5) | 11 |
| [34.5,37.5) | 10 |
| [37.5,40.5) | 5 |
| [40.5,43.5] | 4 |
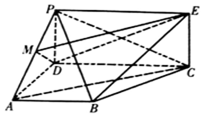 如图,四边形PDCE为矩形,四边形ABCD为梯形,平面PDCE⊥平面ABCD,∠BAD=∠ADC=90°,AB=AD=$\frac{1}{2}$CD=1.
如图,四边形PDCE为矩形,四边形ABCD为梯形,平面PDCE⊥平面ABCD,∠BAD=∠ADC=90°,AB=AD=$\frac{1}{2}$CD=1.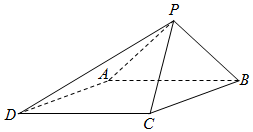 如图,已知四棱锥P-ABCD的底面为菱形,∠BCD=120°,AB=PC=2,$AP=BP=\sqrt{2}$.
如图,已知四棱锥P-ABCD的底面为菱形,∠BCD=120°,AB=PC=2,$AP=BP=\sqrt{2}$.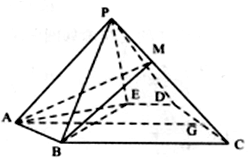 如图,在五棱锥P-ABCDE中,△ABE是等边三角形,四边形BCDE是直角梯形且∠DEB=∠CBE=90°,G是CD的中点,点P在底面的射影落在线段AG上.
如图,在五棱锥P-ABCDE中,△ABE是等边三角形,四边形BCDE是直角梯形且∠DEB=∠CBE=90°,G是CD的中点,点P在底面的射影落在线段AG上.