题目内容

在四面体A-BCD中，共顶点A的三条棱两两互相垂直，且AB=AC=1，AD=
2
若四面体的四个顶点在一个球面上，则B，D的球面距离为______．
∵四面体A-BCD中，共顶点A的三条棱两两互相垂直，且AB=AC=1，AD=
2

故四面体的外接球即为以AB，AC，AD为长宽高的长方体的外接球
可求得此长方体的体对角线长为2
则球半径R=1
弦BD=
3

则cos∠BOD=
OB2+OD2-BD2
2OB•OD
=
1+1-3
2
=-
1
2

∴球心角∠BOD=120°
故B，D的球面距离为
120°
360°
•2π×1=
2π
3

故答案为：
2π
3
练习册系列答案
相关题目
15、在平面几何里有射影定理：设△ABC的两边AB⊥AC，D是A点在BC边上的射影，则AB2=BD•BC．拓展到空间，在四面体A-BCD中，DA⊥面ABC，点O是A在面BCD内的射影，且O在△BCD内，类比平面三角形射影定理，△ABC，△BOC，△BDC三者面积之间关系为
（S△ABC）2=S△BOC．S△BDC
．
在四面体A-BCD中，共顶点A的三条棱两两互相垂直，且AB=AC=1，AD=
2
若四面体的四个顶点在一个球面上，则B，D的球面距离为
2π
3
2π
3
．
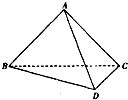（2009•武汉模拟）如图，在四面体A-BCD中，AB=AD=
2
，BD=2，DC=1，且BD⊥DC，二面角A-BD-C大小为60°．
（1）求证：平面ABC上平面BCD；
（2）求直线CD与平面ABC所成角的正弦值．
我们知道，在△ABC中，记D、E、F分别为BC、CA、AB的中点，则：①．AD、BE、CF相交于一点；②．该点将对应线段分成2：1两部分；类比这一结论，在四面体A-BCD中，记G1、G2、G3、G4分别为△BCD、△CDA、△DAB、△ABC的重心，则有结论：①
AG1、BG2、CG3、DG4交于一点
AG1、BG2、CG3、DG4交于一点
；②
该点将对应线段分成3：1两部分
该点将对应线段分成3：1两部分
．
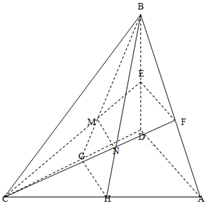精英家教网如图，在四面体A-BCD中，有CB=CD，平面ABD⊥平面BCD，点E、F分别为BD，AB的中点，MN∥平面ABD．
（1）求证：平面ABD⊥平面EFC；
（2）如图，求证：直线MN∥直线GH．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网