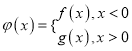题目内容
【题目】已知单调等比数列![]() ,首项为
,首项为![]() ,其前
,其前![]() 项和是
项和是![]() ,且
,且![]() ,
,![]() ,
,![]() 成等差数列,数列
成等差数列,数列![]() 满足条件
满足条件![]()
(1)求数列![]() 、
、![]() 的通项公式;
的通项公式;
(2)设![]() ,记数列
,记数列![]() 的前
的前![]() 项和是
项和是![]() .
.
①求![]() ;
;
②求正整数![]() ,使得对任意
,使得对任意![]() ,均有
,均有![]() .
.
【答案】(1) ,
,![]() ;(2)①.
;(2)①.![]() ;②.
;②.![]() .
.
【解析】
(1)由递推关系首先求得数列![]() 的公比,然后可得其通项公式,利用数列
的公比,然后可得其通项公式,利用数列![]() 的递推关系结合
的递推关系结合![]() 计算可得数列
计算可得数列![]() 的通项公式;
的通项公式;
(2)①.首先整理数列![]() 的通项公式,然后利用分组求和的方法可得其前n项和
的通项公式,然后利用分组求和的方法可得其前n项和![]() ;
;
②.计算![]() 的值,利用函数增长速度的知识和不等式的解集即可确定k的值.
的值,利用函数增长速度的知识和不等式的解集即可确定k的值.
(1)设![]() .由已知得
.由已知得![]() ,即
,即![]() ,
,
进而有![]() .所以
.所以![]() ,即
,即![]() ,则
,则![]() .
.
由已知数列![]() 是单调等比数列,且
是单调等比数列,且![]() ,所以取
,所以取![]() .
.
数列![]() 的通项公式为
的通项公式为 .
.
![]() ,
,![]() ,
,
则![]() .
.
即数列![]() 的通项公式为
的通项公式为![]() .
.
(2)①.由(1)可得:![]() ,
,
分组求和可得:![]() .
.
②由于![]() ,
,
由于![]() 比
比![]() 变化快,所以令
变化快,所以令![]() 得
得![]() .
.
即![]() 递增,而
递增,而![]() 递减。所以,
递减。所以,![]() 最大.
最大.
即当![]() 时,
时,![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目