Question

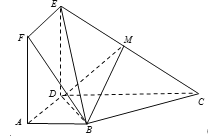
【题目】如图,正方形与梯形所在的平面互相垂直， ，,点在线段上.

(Ⅰ) 若点为的中点，求证：平面；

(Ⅱ) 求证：平面平面；

(Ⅲ) 当平面与平面所成二面角的余弦值为时，求的长.

Answer 1

【答案】(1)证明见解析；(2)证明见解析；(3).

【解析】

(1)建立空间直角坐标系，利用空间向量的结论可证得BM⊥平面ADEF的法向量，从而可证得线面平行；

(2)分别求得平面，平面的法向量，由法向量的数量积为0可证得面面垂直；

(3)设，由题意可得点M的坐标，分别求得两个半平面的法向量，由二面角的余弦值得到关于的方程，解方程求得的值即可确定的长.

(1)∵正方形ADEF与梯形ABCD所在的平面互相垂直，AD为交线，

∴ED⊥平面ABCD，由已知得DA，DE，DC两两垂直，

如图建系D-xyz，可得D(0，0，0)，A(1，0，0)，B(1，1，0)，C(0，2，0)，E(0，0，1)，F(1，0，1).

由M为C的中点，知，故.

易知平面ADEF的法向量为，

，

∵BM平面ADEF，∴BM//平面ADEF.

(2)由(1)知，

设平面BDE的法向量为，

平面BEC的法向量为，

由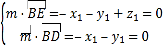得，

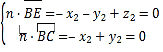由得，

，故平面BDE⊥平面BEC.

(3)设，设，计算可得，

则，

设平面BDM的法向量为，

由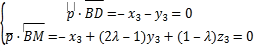得，

易知平面ABF的法向量为，

由已知得 ，

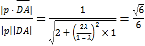解得，此时，

，则，即AM的长为.