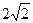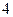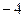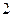题目内容
(本小题满分12分)过抛物线y2=2px(p>0)的焦点F的直线与抛物线交于A、B两点,O为坐标原点,直线OA 的斜率为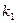 ,直线OB的斜率为
,直线OB的斜率为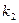 .
.
(1)求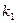 ·
·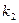 的值;
的值;
(2)由A、B两点向准线做垂线,垂足分别为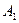 、
、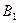 ,求
,求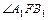 的大小.
的大小.
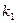 ,直线OB的斜率为
,直线OB的斜率为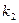 .
.(1)求
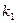 ·
·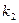 的值;
的值;(2)由A、B两点向准线做垂线,垂足分别为
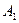 、
、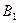 ,求
,求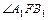 的大小.
的大小.(1)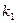 ·
·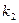 =-4
=-4
(2)
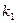 ·
·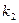 =-4
=-4(2)

解:设A( ),B
),B ),则
),则 ,
, ,
,
∵直线AB过焦点F,若直线AB与x轴不垂直,∴可设AB方程为:y=k( ),代入抛物线方程有
),代入抛物线方程有
 ,可得
,可得 ·
· =
= ,则
,则 ·
· =-p2,
=-p2,
∴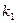 ·
·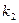 =
= ;若直线AB与x轴垂直,得
;若直线AB与x轴垂直,得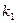 ="2,"
="2,"  ,∴
,∴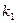 ·
·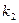 =-4…6分
=-4…6分
(2) 如图,

∵ A、B在抛物线上,∴ |AF|=|AA1|
∴∠AA1F=∠AFA1,∴∠AFA1=
同理
∴
 90o,
90o,
又 ,
,
 . ……12分
. ……12分
 ),B
),B ),则
),则 ,
, ,
,∵直线AB过焦点F,若直线AB与x轴不垂直,∴可设AB方程为:y=k(
 ),代入抛物线方程有
),代入抛物线方程有 ,可得
,可得 ·
· =
= ,则
,则 ·
· =-p2,
=-p2,∴
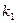 ·
·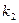 =
= ;若直线AB与x轴垂直,得
;若直线AB与x轴垂直,得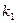 ="2,"
="2,"  ,∴
,∴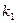 ·
·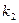 =-4…6分
=-4…6分(2) 如图,

∵ A、B在抛物线上,∴ |AF|=|AA1|
∴∠AA1F=∠AFA1,∴∠AFA1=

同理

∴

 90o,
90o,又
 ,
, . ……12分
. ……12分
练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
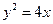 ,F是焦点,直线l是经过点F的任意直线.
,F是焦点,直线l是经过点F的任意直线.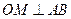 (O是坐标原点,M是垂足),求动点M的轨迹方程;
(O是坐标原点,M是垂足),求动点M的轨迹方程;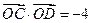 ,求证直线CD必过定点,并求出定点的坐标.
,求证直线CD必过定点,并求出定点的坐标. 的焦点
的焦点 的直线交抛物线于
的直线交抛物线于 两点。
两点。 为定值;
为定值; 为定值.
为定值. 是抛物线
是抛物线 上一动点,则点
上一动点,则点 的距离与
的距离与 的距离和的最小值是 ( )
的距离和的最小值是 ( )


 上一点
上一点 到其焦点的距离为
到其焦点的距离为 ,双曲线
,双曲线 的左顶点为
的左顶点为 ,若双曲线一条渐近线与直线
,若双曲线一条渐近线与直线 平行,则实数
平行,则实数 等于( )
等于( )



 的焦点坐标为_______________;准线方程为_______________.
的焦点坐标为_______________;准线方程为_______________.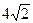
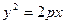 的焦点与双曲线
的焦点与双曲线 的右焦点重合,则
的右焦点重合,则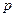 的值为( )
的值为( )