题目内容
某同学研究sinx+cosx时,得到如下结果:
①sinx+cosx=
sin(x+
);②sinx+cosx=
sin(x-
);
③sinx+cosx=
cos(x+
);④sinx+cosx=
cos(x-
).其中正确的个数有( )
①sinx+cosx=
| 2 |
| π |
| 4 |
| 2 |
| π |
| 4 |
③sinx+cosx=
| 2 |
| π |
| 4 |
| 2 |
| π |
| 4 |
| A、1个 | B、2个 | C、3个 | D、4个 |
分析:从sinx+cosx中提出
,若将
分别看成cos
,sin
则用两角和的正弦公式化简;若将
分别看成cos
,cos
则用两角差的余弦公式化简.
| 2 |
| ||
| 2 |
| π |
| 4 |
| π |
| 4 |
| ||
| 2 |
| π |
| 4 |
| π |
| 4 |
解答:解:sinx+cosx=
(
sinx+
cosx)=
(cos
sinx+sin
cosx)=
sin(x+
);
或sinx+cosx=
(
sinx+
cosx)=
(sin
sinx+cos
cosx)=
cos(x-
);
故①④正确.
| 2 |
| ||
| 2 |
| ||
| 2 |
| 2 |
| π |
| 4 |
| π |
| 4 |
| 2 |
| π |
| 4 |
或sinx+cosx=
| 2 |
| ||
| 2 |
| ||
| 2 |
| 2 |
| π |
| 4 |
| π |
| 4 |
| 2 |
| π |
| 4 |
故①④正确.
点评:本题考查利用两角和差的正弦、余弦公式化简:asinx+bcosx=
sin(x+α)
| a2+b2 |

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
 ;②
;② ;
; ;④
;④ .
.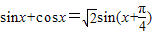 ;②
;②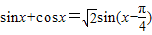 ;
;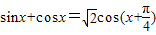 ;④
;④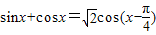 .其中正确的个数有( )
.其中正确的个数有( )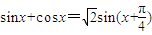 ;②
;②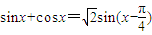 ;
;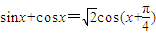 ;④
;④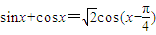 .其中正确的个数有( )
.其中正确的个数有( )